因果関係を調べる際に有効なランダム化比較試験について,図と具体例を用いて解説します.
ランダム化比較試験の目的やデメリットについても解説しています.
ランダム化比較試験とは
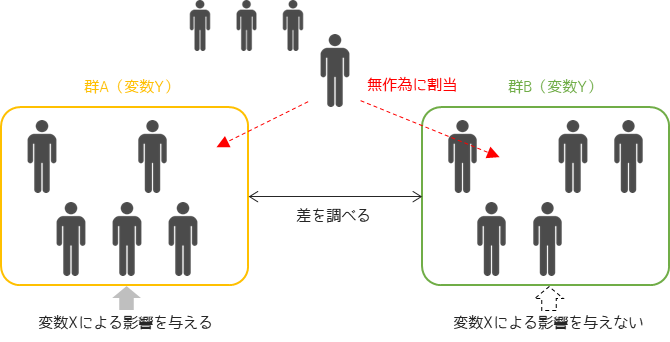
ランダム化比較試験(Random Control Trial, RCT)とは,サンプルを無作為に割当てた異なる群に対して,変数X(要因)の介入度を変えた結果変数Y(結果)が群ごとにどれだけ差があるかを調べる手法です.
例えばWebサイトのユーザテストでは,デザイン(変数X)だけ異なる2つのサイトを用意してランダムに訪問者を割り当てます.訪問者に対して行ったユーザビリティに関するアンケート結果(変数Y)から,デザインの違いがどれだけユーザビリティに影響を与えているかを調べることができます.
ランダム化比較試験をビジネスでは,ABテストと呼ぶことも多いです.
なぜランダム化比較試験を行うのか
ランダム化比較試験を行わない場合の問題点
ランダム化比較試験の目的は変数Xから変数Yの因果効果を調べることです.異なる群を比較する際にランダム化比較試験を行わない場合,以下のような問題が発生します.
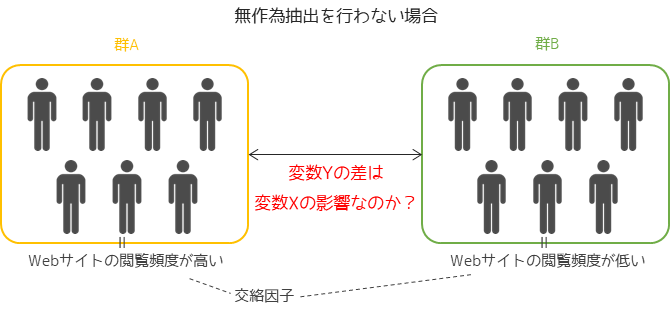
無作為抽出を行わないWebサイトのユーザテストの例では,群Aには普段からWebをよく閲覧する傾向があるが,群Bは閲覧頻度が低い傾向があるというような偏りが生まれる可能性があります.
アンケートの結果から群Aが訪問したWebサイトの方が,ユーザビリティが良いという結果(変数Y)が出た場合でも,それはユーザ属性の違いが影響している可能性があり,デザイン(変数X)による影響であると結論づけるのことが難しくなります.
この偏りの原因を交絡因子と言い,調べたい要因以外に交絡因子が含まれると因果効果の推定が困難になります.
交絡因子を完全に排除する方法
変数Xによる影響のみを調べたい場合,交絡因子を全て取り除く必要があります.
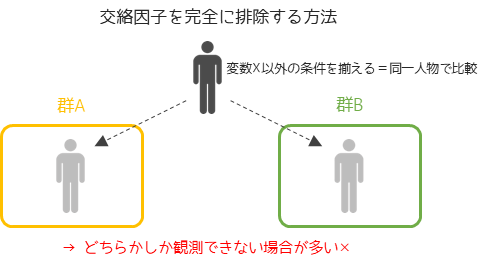
交絡因子は調べたい変数X以外の条件を全て揃えることで,完全に排除することができます.しかし,条件を全て揃えるためには同一人物(個体)かつ同じ状態(時間)で比較する必要があり,現実では不可能な場合が多いです.異なるWebサイトを同じ状態で訪問することができません.必ずどちらかの潜入感がある状態で他方のサイトを訪問することになります.これを因果推論の根本問題と言います.
無作為抽出による交絡因子の排除
因果推論の根本問題から個人で変数X以外の条件を揃えることは難しいため,集団として交絡因子を排除する方法がランダム化比較試験になります.
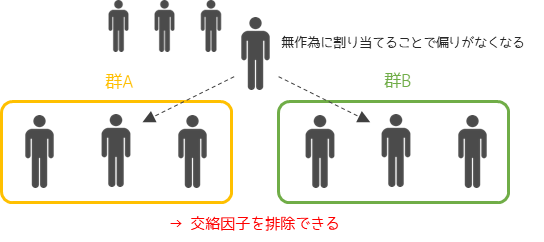
無作為の割り当てることで,群Aと群Bの偏りがなくなるつまり条件を揃えることができます.これにより交絡因子は排除されるため,結果(変数Y)の差は調べたい要因(変数X)による影響であると考えることができます.
統計学では無作為抽出を行った群間に対して,t検定などの仮説検定で差を比較して因果関係を調べます.
ランダム化比較試験の限界
因果関係を調べる際に,交絡因子を排除する方法としてランダム化比較試験は強力です.
しかし,ランダム化比較試験がどのような状況でも行えるわけではありません.ランダム化比較試験には2つのデメリットがあります.
① 倫理的な問題
例えば健康に関する調査を行うために,喫煙の有無による健康状態の差を調べるとします.ランダム化比較試験を行うとすると,無作為に被験者を選択して片方の被験者には喫煙させてその後の健康状態を追跡する必要があります.このように,被験者に対して悪影響を与える可能性がある実験を行うことは倫理的に難しいです.
② 事前に介入する必要性
ランダム化比較試験を行うためには,調べたい要因が影響を与える前に無作為抽出を行い,要因による影響の調査が完了するまで制御・追跡する必要があります.これは要因による影響が長期的な場合などに難しくなります.このような場合にランダム化比較試験を行うと実験に対してコストがかかり,サンプルサイズを大きくすることは難しいです.
計画的な実験・データ分析では無い限り,実験を行う前に無作為抽出をすることはありません.加えて自分で実験を行わない場合つまり,既存のデータで分析を行う場合はランダム化比較試験を行うことは不可能です.
ランダム化比較試験を行わずに,因果関係を推測する(交絡因子を排除する)方法として統計的因果推論や統計的因果探索という手法があります.
統計的因果推論
統計的因果推論は既存のデータに対して,交絡因子を排除する方法です.具体的には共分散分析や層別解析,傾向スコアマッチングといった方法があります.









