メタアナリシスとは
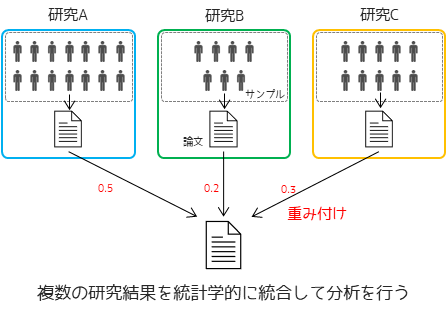
メタアナリシスとは,複数の研究結果(学術論文)を統計学的に統合して,分析を行う手法です.特に医学分野の研究でよく用いられる手法で,例えば飲酒習慣とがん発症の関連性に関する既存研究が複数あった場合に,それらの研究結果(p値など)を統合して新たに関連性を判断したりします.統合する際には単に平均値を取るのではなく,各研究に重み付けを行うのがメタアナリシス特有の分析手法になります.
メタアナリシスには通常の研究・統計解析と比較して,以下のようなメリットがあります.
・サンプルサイズが大きくなり,検出力が向上する
・実験を行う必要がない
・研究間の結果を比較することで,特定の介入や知見がどの程度一般化可能か判断するできる
・出版バイアスや選択バイアスなどの問題を特定できる
メタアナリシスを行う目的で特に重要なのが,最初の2つになります.学術論文を作成するために新たに実験を行うには,莫大な時間とお金が必要となります.特に医学分野において,ある程度のサンプルサイズを確保した上で臨床研究を行うのは非常に大変です.
メタアナリシスにおいては,既存研究を用いるため新たな実験は不要で,サンプルサイズも確保することができます.つまり,研究費に余裕がない方や楽して学術論文を作成したい方にとって最適な分析手法であるとも言えます.
メタアナリシスの信頼性
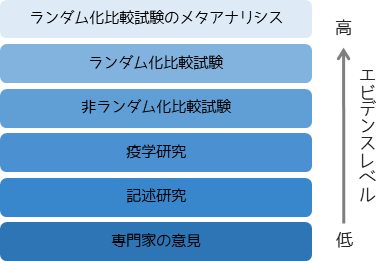
メタアナリシスのエビデンスレベルは非常に高いとされています.エビデンスレベルとは,真の値から誤差が小さいこと,つまり研究結果にバイアスが含まれていないことを意味します.
バイアスを取り除くことができる実験方法として,ランダム化比較試験(RCT)がありますが,それらの結果を包括的に分析を行うメタアナリシスはRCTよりエビデンスレベルが高いとされます.
ただし,高いエビデンスレベルを保ったメタアナリシスを行うためには,対象となる学術論文の選定から分析まで正確に行う必要があります.
メタアナリシスとシステマティックレビュー

システマティックレビュー(SR)は,似たような意味で用いられることもありますが,狭義ではシステマティックレビューの中で,統計解析のような定量的に分析を行う手法をメタアナリシスと言います.
システマティックレビューとは,特定の命題に関する既存研究から厳選を行い分析を行う手法です.統計学を用いた分析以外にも,既存研究の数や手法,背景など定性的に整理することも含まれます.
メタアナリシスの手順
メタアナリシスは具体的に以下のような手順で実施するのが一般的です.
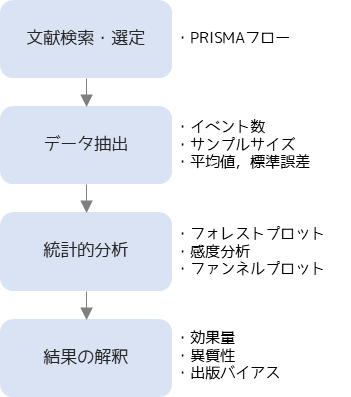
PRISMA(Preferred Reporting Items for Systematic Reviews and Meta-Analyses)とは,システマティックレビューやメタアナリシスの報告の質を向上させるためのガイドラインです.
特に,学術誌の投稿を行う場合は,文献検索・選定の手順をPRISMAフローの沿って行い,その結果をPRISMAフロー図として記載することが多いです.
データ抽象ではメタアナリシスに必要な値を,文献から読み取り整理します.メタアナリシスでは,統合的な効果量としてオッズ比やリスク比,平均差を扱うことが多いため,それらの値に必要な処置群・統制群ごとのイベント数やサンプルサイズを整理します.具体的に必要なデータはこの後の節に記載しています.
抽出したデータから統合的な効果量を算出するために,固定効果モデルや変量効果モデルを用います.算出した効果量・信頼区間は,選定した文献ごとの効果量と並べて比較するためにフォレストプロットを作成します.フォレストプロットには異質性検定の結果なども記載することが多いです.
結果の解釈では,フォレストプロットや異質性検定の結果を用いて,文献間の結果に一貫性があるか判断を行います.また,ファンネルプロットから出版バイアスの有無を判断して,最終的には算出した統合的な効果量がどれぐらい信頼性が高いか評価します.
メタアナリシスの実行方法
メタアナリシスは,統合効果の算出や重みに比例したプロットが必要なため,Excelなどの表計算ソフトで作成することは難しいです.メタアナリシスはRやPythonなど,統計用ソフトで実行されます.
統計解析アプリStaatAppでは,分析対象のデータを読み込み,クリックするだけで簡単にメタアナリシスの実行,グラフ作成をすることができます.
初めての方はメタアナリシス機能を含むほぼ全ての機能を無料で利用できるので,お気軽にダウンロードしてお使いください!
》StaatAppを用いたメタアナリシス
》統計解析アプリStaatApp
メタアナリシスで扱う統計量・データ
メタアナリシスでは,以下の統計量(効果量)を扱うことが多いです.

分析対象のデータがカテゴリーデータである場合は,クロス集計表からオッズ比やリスク比が分析結果として算出されることが多いです.特に医学分野の研究ではよく用いられ,メタアナリシスの対象となる効果量としてもよく使用されます.
分析対象のデータが数量データである場合は平均差や標準化平均差が,生存時間データである場合はハザード比が効果量として用いられます.
データ抽出の段階で,対象の研究の生データ(各サンプルの観測結果など)を文献から得られることはまずありません.そのため,メタアナリシスを行うためには計画した効果量・信頼区間を算出するために必要な統計量を,文献から抽出する必要があります.
各統計量に対して,抽出が必要なデータは以下のようになります.

例えば,統合効果を平均差としてメタアナリシスしたい場合は,各群のサンプルサイズは必須データで,各群の平均値と標準誤差もしくは全体の効果量(平均差)と標準誤差が必要となります.
ハザード比を除く統計量では,各群の値を抽出して計算することが望ましいですが,文献によって全体の値のみ抽出できる場合は,全文献のデータを全体の値に換算してからメタアナリシスを行います.
また,標準誤差については記載されている信頼区間から算出することができます.
具体的なメタアナリシスの手順については,以下のページで紹介しています.
メタアナリシスにおける統合効果
メタアナリシスにおいて,統合効果を算出する方法は固定効果モデル(Fixed-effect model)と変量効果モデル(Random-effect model)に分類されます.
| 特徴 | 選択基準(参考) | |
| 固定効果モデル | ・重みがサンプルサイズ/イベント数にほぼ比例 ・統合する研究結果は全て同一であると仮定 ・異質性が大きい場合,統合効果の信頼区間が小さくなる | ・研究数が少ない場合 ・出版バイアスを避けたい場合 |
| 変量効果モデル | ・統合する研究結果にばらつきがあると仮定 ・異質性が大きい場合,統合効果の信頼区間が大きくなる | ・異質性が大きい場合(I²>50%) ・第一種の過誤を避けたい場合 |
それぞれのモデルは各研究のばらつきを許容するかという点で,統合効果の算出方法が異なります.一般的に異質性(研究間のばらつき)が大きい場合は,変量効果モデルが採用されます.異質性尺度 I²>50%以上の場合に,変量効果モデルを採用する論文がありますが,明確な基準があるわけではありません.
異質性が大きい場合に,統合効果の信頼区間が変量効果モデルの方が小さくなることから,第一種の過誤を避けたい場合に,変量効果モデルを採用するという考え方もあります.
各モデルでよく用いられる統合効果の算出手法は,以下のようになります.
| オッズ比/リスク比/リスク差 | 平均差/標準化平均差/ハザード比 | |
| 固定効果モデル | Mantel-Haenszel法 | 一般化逆分散法 |
| 変量効果モデル | DerSimonian-Laird法 | DerSimonian-Laird法 |
Rなどの統計ソフトでは,上記の算出方法がデフォルトで設定されています.StaatAppでも上記の手法で統合効果の算出を行っています.
平均値を統合効果として扱う場合,例えば研究間のサンプルサイズに大きな差があった場合でも,同じ精度の結果として扱ってしまうことになります.サンプルサイズが小さい研究結果のみで,有効なイベント数が異常に多い場合に,その結果が影響して統合効果も有効という結果になる可能性があります.
そのためメタアナリシスの基本的な考え方として,有効数と無効数の“差”を効果量として扱います.差であればサンプルサイズが小さい研究は,大きな差が発生しないため統合効果への影響が小さくなります.加えて重み付けを行うことで,よりサンプルサイズが大きい研究結果の影響を考慮することができます.
メタアナリシスにおける異質性
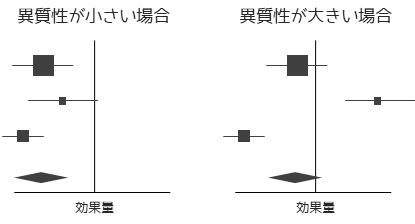
メタアナリシスにおける異質性とは、異なる研究間で効果量の結果にばらつきが見られる現象を指します.異質性が大きいということは,各研究が同一の効果量を持っていない可能性があることを示しており,このばらつきは研究計画や,介入の方法,結果の測定方法など多くの要因によって生じることがあります.
異質性を評価する方法としては,グラフを用いる方法と統計的手法を用いる方法があります.グラフを用いる方法では,図のようなフォレストプロットを用いて視覚的に判断を行います.
統計的手法の代表例としては,コクランのQ検定と異質性尺度 I² を用いる方法が一般的です.
コクランのQ検定では,各研究の重みと効果量,統合効果からp値を算出します.一般的な仮説検定ではp<0.05である場合に有意であると判断しますが,異質性の検定では,0.1未満である場合に,統計的有意=異質性がある可能性が高いと判断します.ただし,サンプルサイズが大きいほど有意になりやすい傾向があります.
異質性尺度 I² はコクランのQ検定のQ統計量をサンプルサイズで調整した値で,0から100までの値を取ります.目安として,I² = 0 で異質性なし,60%以上でそこそこの異質性がある,85%以上で高度の異質性があると判断できます.
また,I² = 0 の場合,固定効果モデルと変量効果モデルの算出結果は完全に一致します.
メタアナリシスで用いるグラフ
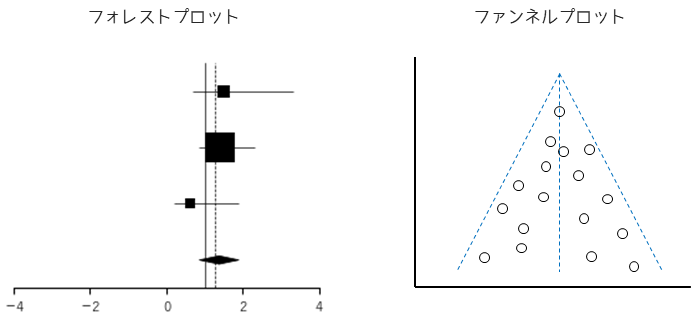
メタアナリシスでは,フォレストプロットとファンネルプロットの2つのグラフがよく用いられます.フォレストプロットは前述の通り,各研究の効果量を視覚的に比較するために用いられます.ファンネルプロットは,メタアナリシスにおいて重要な観点である出版バイアスを確認するために用いられます.
これらのグラフについては,以下のページで詳しく紹介しています.










