級内相関係数

級内相関係数とは

級内相関係数（Intraclass Correlation Coefficient; ICC）とは，一般的な相関係数（ピアソンの積率相関係数）とは異なり，データそのもの一致度を調べるための統計的指標値です．

医学分野における一例としては，ある放射線医が同じ画像を異なる時点で独立して評価する際に，一貫性を測定する場合に用います．

心理学分野では，複数の評価者（研究者や臨床心理士）が同じ被験者や患者について独立して評価を行った場合に，その評価の一貫性を測定する場合に用います．

級内相関係数係数には，６つの種類があります．

・ICC(1,1)
・ICC(1,k)
・ICC(2,1)
・ICC(2,k)
・ICC(3,1)
・ICC(3,k)

医学分野の例はICC(1,1)で，検者内信頼性とも表現されます．心理学分野の例はICC(2,1)を用いる例で，検者間信頼性とも表現されます．

級内相関係数は０～１の間の値取り，１に近いほど信頼性が高い（＝一致度が高い）と考えることができます．

》相関係数とは

ICC(1,1)

ICC(1,1)は検者内信頼性と表現され，同じ評価者が同じ被験者に対して複数回観測を行った場合の観測値の信頼性になります．

ICC(1,1)が１に近いほど，特定の評価者の評価や測定機器の観測値の再現度が高いことを示します．

観測時点に時間的間隔がある場合に，用いられることが多いです．

ICC(1,k)

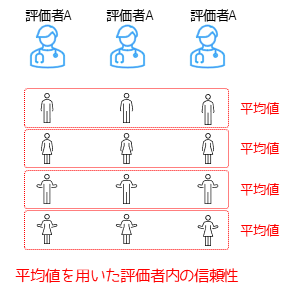
ICC(1,k)は同じ評価者が同じ被験者に対してk回観測を行った場合に，得られた観測値の平均値を用いた信頼性になります．

図のように3回観測を行った場合は，ICC(1,3)と表現されます．

基本的にはICC(1,1)を算出してから，測定した値の平均値にどれだけ信頼性があるか調べる場合にICC(1,k)を算出します．

ICC(2,1)

ICC(2,1)は検者間信頼性と表現され，異なる評価者が同じ被験者に対して観測を行った場合の観測値の信頼性になります．

ICC(2,1)が１に近いほど，複数の評価者や複数の計測機器の観測値の値が一致していることがわかります．

級内相関係数の中でICC(2,1)は最もよく使用され，同じサンプル（観測対象）に対する一致度を調べる場合に幅広く用いられます．

ICC(2,k)

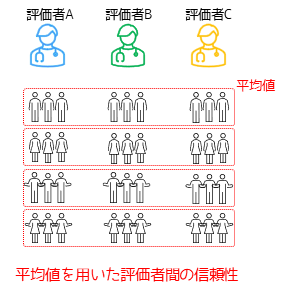
ICC(2,k)は異なる評価者が同じ被験者に対してk回観測を行った場合に，得られた観測値の平均値を用いた検者間信頼性になります．

図のように各評価者が同じ被験者に対して，3回観測を行った平均値に対する場合は，ICC(2,3)と表現されます．

ICC(3,1)

ICC(3,1)もICC(2,1)と同様に検者間信頼性と表現され，異なる評価者が同じ被験者に対して観測を行った場合の観測値の信頼性になります．ICC(2,1)との違いは，各評価者の観測値に一定量の差がある場合にも用いることができます．

例えば，あるコンテストで審査員ごとに評価点の基準が異なり審査員Aは高い値を，審査員Cは低い値を出す傾向があるとします．このような場合，ICC(2,1)では値が低くなり審査員間の一致度は小さいと判定されますが，ICC(3,1)では一定量の差で評価を行っているのであれば１に近い値が算出されます．

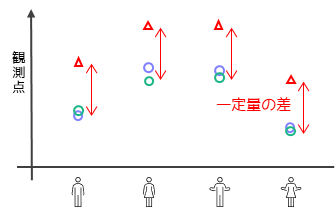
実際には一定間隔で観測点が異なることは稀のため，ICC(3,1)が使用されることはあまりありません．

ICC(3,k)

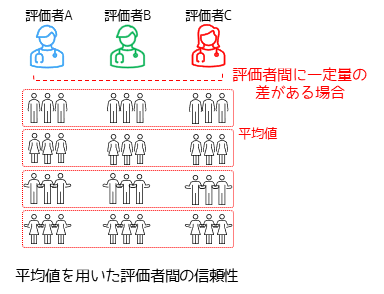
ICC(3,k)は異なる評価者が同じ被験者に対してk回観測を行った場合に，得られた観測値の平均値を用いた検者間信頼性になります．ICC(3,1)と同様に，各評価者の観測値に一定量の差がある場合にも用いることができます．

ICCの目安

級内相関係数には明確に基準はありませんが，一般的な目安は下記になります．

0.00-0.19：slight(非常に軽度の一致)
0.20-0.39：fair(軽度の一致)
0.40-0.59：moderate(中程度の一致)
0.60-0.79：substatial(しっかりとした一致)
0.80-：moderate(ほぼ完全な一致)

これはLandisとKoch(1977)による基準で，理論的な根拠はありません．

0.7を基準にして一致度を判定する場合も多いですが，基本的には分野の既往研究と比較して評価するのがベターです．

ICCの算出方法

ICCを算出するためには，被験者間変動や測定ごとの誤差などを算出する必要があります．これらの値は二元配置分析分析を行うことで計算できますが，Excelなどの表計算ソフトで算出するには手間がかかり，誤った計算をしてしまう可能性があります．

統計解析アプリStaatAppでは，分析対象のデータを読み込み，クリックするだけで簡単に級内相関係数や信頼区間を求めることができます．級内相関係数以外にも様々な統計解析やグラフ作成が気軽に行うことができます．

》StaatAppを用いた級内相関係数の算出
》統計解析アプリStaatApp

信頼区間

学術論文などで級内相関係数を記載する場合は，95％信頼区間の上限値・下限値も記載するのが一般的です．

級内相関係数が非常に小さい値の場合は，信頼区間の下限値は負の値になることもあります．同様に，上限値も１を超える場合がありますが，級内相関係数（点推定）は１を超えることはないので，上限値＝１とする場合もあります．

StaatAppではそれぞれの級内相関係数に対して，95％信頼区間の上限値・下限値が同時に算出されます．

誤用注意！組み合わせた使い方

ICCは複数の種類を合わせて使用する場合もあります．

例えば，二人の評価者が同じ被験者に対して３回評価を行ったとします．評価結果を表に整理すると以下のようになります．

評価者ごとの信頼性を調べるために，ICC(1,1)とICC(1,3)を算出します．評価者AのICC(1,1)とICC(1,3)を算出する場合は，評価者Aの１回目から３回目のデータを用いて計算を行います．

・評価者A　　ICC(1,1)：0.89　　ICC(1,3)：0.92
・評価者B　　ICC(1,1)：0.81　　ICC(1,3)：0.88

このような値が算出された場合，各評価者の信頼性は十分に高いと言えます．

次に評価者間での信頼性を調べるために，ICC(2,1)とICC(2,2)を算出します．ICC(2,1)とICC(2,2)を算出する場合は，各評価者の平均値を用いて計算を行います．同じ被験者に対して複数回観測を行った場合に，１回目や２回目のデータを用いてICC(2,1)を算出するのは誤りになるので注意が必要です．

　　　　　　 ICC(1,1)：0.84　　ICC(1,3)：0.85

上記のような結果が得られた場合，評価者ごとの評価結果に対しても信頼性があると判断することができます．