説明変数と目的変数

説明変数とは

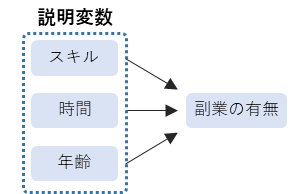
説明変数とは，結果に影響を与えている要因を意味します．

例えば，「副業をしてる」という結果に対して，副業を行う「スキルがある」かや「時間がある」かといったデータは要因になります．

数式的に説明すると，「 y = αx + β 」の「ｘ」に代入するデータを説明変数と言います．

説明変数は，以下のような呼ばれ方をすることも多いです．

・予測変数
・独立変数
・共変量

“共変量”はランダム化された実験や，臨床試験の文脈でよく使用されます．実験の結果に影響を与える可能性があるが，研究者が直接制御できない変数を指すことが多いです．例えば，患者の年齢や体重などが共変量として考慮されることがあります．

目的変数とは

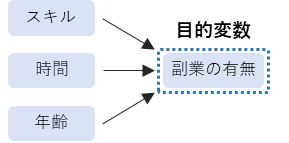
目的変数とは，要因から影響を受けて起きた結果を意味します．

説明変数とは反対に，副業を行う「スキルがある」かや「時間がある」かといった要因の影響を受けて「副業をしているか」というのが結果になります．

数式的には，「 y = αx + β 」の「ｘ」を代入した際に求められる「ｙ」を目的変数と言います．

目的変数は，以下のような呼ばれ方をすることも多いです．

・応答変数
・反応変数
・従属変数
・基準変数
・被説明変数

説明変数と目的変数の選び方

説明変数と目的変数の選び方の観点は2つになります．

① 因果関係を調べたい場合

因果関係を調べたい場合，扱うデータのうち結果となるデータを目的変数として，それ以外のデータを説明変数とします．

ここで注意すべき点は，データ収集する段階から結果と要因の関係を意識することです．

例えば，「年収」・「年齢」・「役職」といったデータがあるとします．３つのデータは互いに関連性があり，どれが結果（目的変数）となるか決めることができません．

仮に日本的な企業で，「年齢」が上がるにつれて賃金が上がる場合は「年収」を目的変数として考えることもできます．

② 予測したい場合

回帰分析などの結果から，ある値を予測したい場合は予測のもととなるデータを説明変数に，予測したいデータを目的変数にします．

例えば，「年齢」から「年収」を予測したい場合は「年齢」を説明変数に，「年収」を目的変数にして単回帰分析を行います．結果から得られた回帰モデルに，「年齢」を代入することで「年収」を予測することができます．

因果関係を調べたい場合と違い，説明変数と目的変数の因果関係の方向は気にする必要はありません．