クラメールの連関係数とは
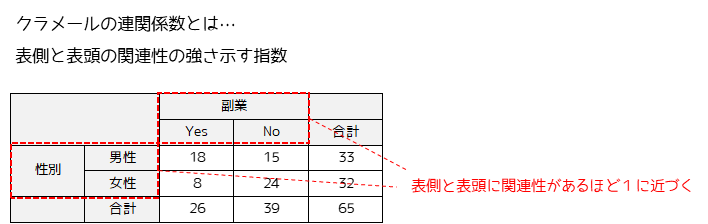
クラメールの連関係数とはクロス集計表の2項目の関連性の強さを表す指標です.
0から1の間の値を取り,1に近いほど2項目の関連性が強いと言うことができます.
類似した統計量として相関係数があります.相関係数については以下のページで解説しています.
例題の設定
例題では以下のサンプルデータを用います.社会人65人に対して副業の有無を調査した例です.
| No. | 性別 | 副業 |
|---|---|---|
| 1 | 女性 | してない |
| 2 | 男性 | してる |
| 3 | 女性 | してない |
| 4 | 女性 | してない |
| 5 | 男性 | してない |
| 6 | 女性 | してる |
| 7 | 女性 | してない |
| 8 | 女性 | してない |
| 9 | 女性 | してない |
| 10 | 女性 | してない |
| 11 | 男性 | してる |
| 12 | 女性 | してない |
| 13 | 男性 | してない |
| 14 | 女性 | してない |
| 15 | 女性 | してない |
| 16 | 男性 | してない |
| 17 | 男性 | してる |
| 18 | 男性 | してない |
| 19 | 男性 | してない |
| 20 | 女性 | してる |
| 21 | 男性 | してない |
| 22 | 女性 | してない |
| 23 | 女性 | してない |
| 24 | 女性 | してる |
| 25 | 女性 | してない |
| 26 | 男性 | してる |
| 27 | 男性 | してる |
| 28 | 女性 | してる |
| 29 | 男性 | してる |
| 30 | 男性 | してる |
| 31 | 女性 | してない |
| 32 | 女性 | してない |
| 33 | 男性 | してる |
| 34 | 女性 | してる |
| 35 | 男性 | してない |
| 36 | 男性 | してる |
| 37 | 女性 | してない |
| 38 | 女性 | してる |
| 39 | 男性 | してない |
| 40 | 女性 | してる |
| 41 | 男性 | してない |
| 42 | 女性 | してない |
| 43 | 男性 | してる |
| 44 | 男性 | してない |
| 45 | 男性 | してない |
| 46 | 男性 | してる |
| 47 | 女性 | してない |
| 48 | 女性 | してない |
| 49 | 男性 | してない |
| 50 | 男性 | してない |
| 51 | 男性 | してる |
| 52 | 男性 | してる |
| 53 | 男性 | してる |
| 54 | 男性 | してる |
| 55 | 女性 | してない |
| 56 | 男性 | してない |
| 57 | 男性 | してない |
| 58 | 女性 | してる |
| 59 | 女性 | してない |
| 60 | 男性 | してる |
| 61 | 女性 | してない |
| 62 | 男性 | してる |
| 63 | 男性 | してる |
| 64 | 女性 | してない |
| 65 | 女性 | してない |
クラメールの連関係数を求めることで,性別と副業有無の関連性について調べます.
Excelを用いた計算手順
Excelを用いたクラメールの連関係数の計算手順について説明します.
以下のような表を作成して,クラメールの連関係数を求めます.
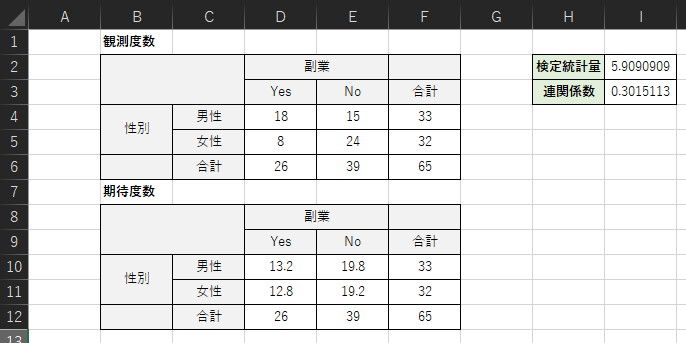
入力式の例は以下になります.
・D10:=D6*F4/F6
・E10:=E6*F4/F6
・D11:=D6*F5/F6
・E11:=E6*F5/F6
・I2:=((D4-D10)^2/D10)+((E4-E10)^2/E10)+((D5-D11)^2/D11)+((E5-E11)^2/E11)
・I3:=SQRT(I2/(F6*1))
計算手順について説明します.
① 観測度数のクロス集計表を作成する【D4-6】【E4-6】【F4-6】
ローデータ(サンプルデータ)からクロス集計表を作成します.Excelを用いたクロス集計表の作成方法についてはこちらのページで解説しています.
② 期待度数を求める【D10-11】【E10-11】
観測度数から各セルの期待度数を求めます.期待度数とは2項目に関連性がない場合はこの値に近づくであろうという値です.
説明のため観測度数のクロス集計表に以下のような記号を付します.
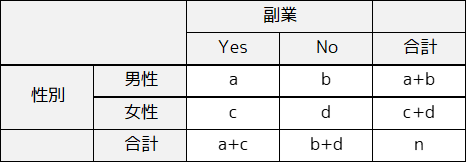
各セルの期待度数は以下の式で求めることができます.

③ 検定統計量Χ2を求める【I2】
検定統計量Χ2は以下の式で求めることができます.

各セルの対応する観測度数から期待度数引いた値を2乗して期待度数で割った値の総和となります.
④ 連関係数vを求める【I3】
クラメールの連関係数vは検定統計量Χ2を用いて以下の式で求めることができます.

nはサンプルサイズ,k(自由度)はクロス集計表における表側と表頭の要素数が小さい方の要素数を示します.分母では理論上最大となる検定統計量を求めています.
例題では連関係数は0.301…となりました.
計算結果を間違えたくない方へ
Excelを用いた計算方法より簡単に,クロス集計表の作成・クラメールの連関係数の計算ができる統計解析アプリStaatAppを販売しております.
StaatAppではクラメールの連関係数以外にもカイ二乗検定やコレスポンデンス分析などのクロス集計表の分析をマウス操作だけ実行することができます.詳細は以下のページをお読みください.
》StaatAppで行うクロス集計表の分析
》統計解析アプリStaatApp
補足① 関連性の強さの目安
クラメールの連関係数は0から1の間の値を取りますが,関連性がある場合でも低めになる傾向があります.関連性の強さの目安は以下になります.
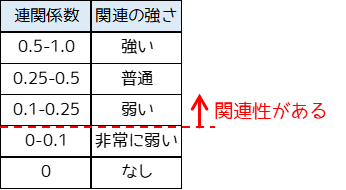
0.1以上の値である場合に,関連性があると言うことが一般的です.
例題では0.301…であったため,「性別と副業の有無に関連性がある」といった結論を得ることができます.
補足② カイ二乗検定との関係
クラメールの連関係数と同様に,クロス集計表の2項目の関係性を調べる方法としてカイ二乗検定(独立性の検定)があります.
カイ二乗検定ではクラメールの連関係数でも求めた検定統計量Χ2の大きさで関連性の判定を行います.
検定統計量Χ2はクロス集計表の総度数やセルの数が増えるにつれて値が大きくなります.クラメールの連関係数はカイ二乗検定の効果量でもあり,純粋に2項目の関連性を調べる方法として有効です.










