回帰分析とは
回帰分析とは,原因を意味する変数xが結果を意味する変数yに与える影響を調べる解析手法です.
そもそも回帰とは,変数xと変数yの間にy=f(x)といった関数に当てはめることです.この関数を回帰式と言い,回帰分析とは具体的には回帰式を求めるための計算を行います.
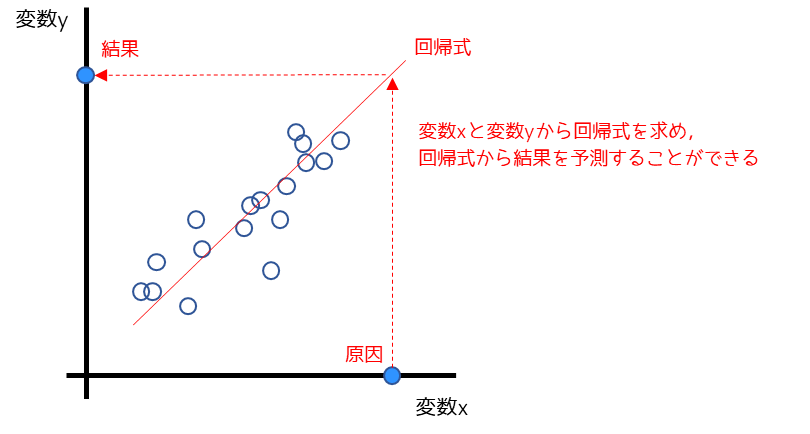
回帰式に原因となる値を代入して結果を予測することも,回帰分析の目的の1つになります.
回帰式は以下のように表されます.
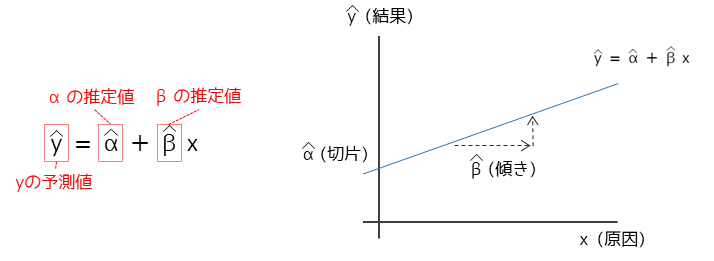
回帰式を定めるパラメータαとβを回帰係数と言います.特に回帰式の傾きを示すβは偏回帰係数とも言います.
結果を表す変数yは目的変数と言い,原因を表す変数xは説明変数と言います.上記の式のように説明変数が1つの回帰式を単回帰式と言います.
原因と結果の関係性を調べ方の応用として因果推論という手法があります.特に最近注目されている手法です.
因果推論とは観測データに対して結果に対する特定の要因のみの影響を調べるための手法です.現実世界では事象と事象は複雑な因果関係があり,特定の要因による影響を調べるためにはそれ以外の要因による影響を取り除く必要があります.
回帰分析の手順
回帰分析は以下のような手順で行います.
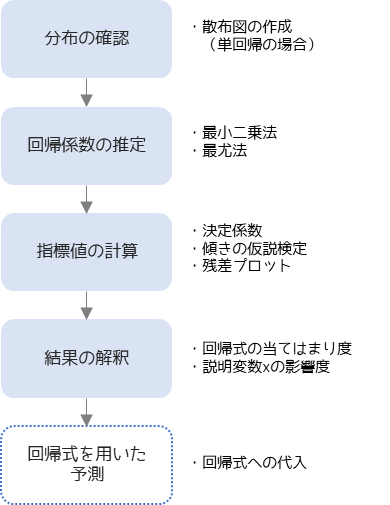
回帰分析の行う前に,扱うデータの分布を確認します.特に説明変数xが1つの単回帰分析を行う場合は,目的変数yと説明変数xの散布図を作成して,外れ値の有無などを確認します.外れ値がある場合は,該当データが正しいか確認を行い明らかに間違ったデータである場合は除外します.
回帰係数の推定では主に最小二乗法を用いて計算を行います.最小二乗法以外には最尤法という計算方法もあります.
回帰係数を推定したら回帰式の当てはまり度や,説明変数xの影響度を統計的に判断するために決定係数などの指標値やグラフを作成します.
計算した指標値を用いて,推定した回帰式の正しさを解釈します.解釈した結果,回帰式が正しいと判断した場合は回帰式を用いて目的変数yの予測を行うことができます.
最小二乗法
最小二乗法とは,回帰式の回帰係数(αとβ)を推定する方法になります.最小二乗法の考え方は以下のようになります.
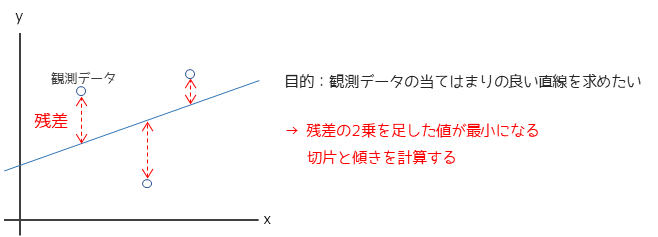
観測データと予測値の差を残差と言い,残差の2乗を足した値(残差平方和)が最小になるαとβを計算する方法を最小二乗法と言います.
αとβの推定値を計算することで回帰式を求めることができます.
回帰分析では目的変数yの残差のみを考えます.相関係数とは異なり説明変数xの分布は関係ありません.
決定係数
決定係数R2は回帰式の当てはまりの良さを示す指標で,寄与率と呼ばれることもあります.決定係数は0から1の間の値をとり,1に近いほど観測データが回帰式によく当てはまっていることを意味します.
決定係数R2は以下の式で定義されます.
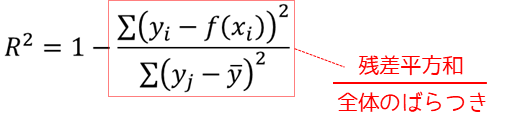
決定係数は1から,目的変数yの残差平方和を観測データ全体のばらつきで割った値の差になります.観測データ全体のばらつきに対して,残差平方和(回帰式と各観測データの距離)が小さい場合決定係数は大きくなります.
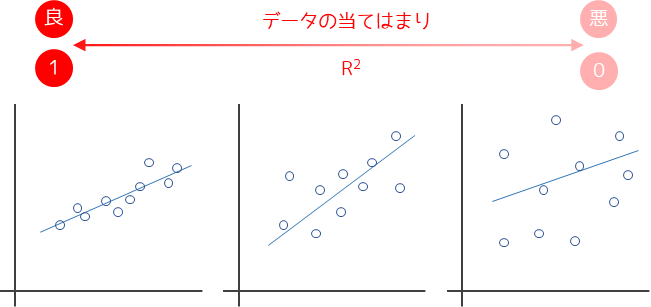
決定係数にはいくつ以上の値を取れば良いかという統計学的な基準はありません.基準は分析者の経験や既往研究から判断します.私の場合はR2>0.6であれば,推定された回帰式の精度がある程度高いと判断して予測に用いることが多いです.
単回帰式の場合,決定係数は目的変数yと説明変数xのピアソンの積率相関係数rの2乗に一致します.
t検定(仮説検定)
推定された回帰式の傾きβが0に近い場合,説明変数xが目的変数yに影響を与えているとは言えません.
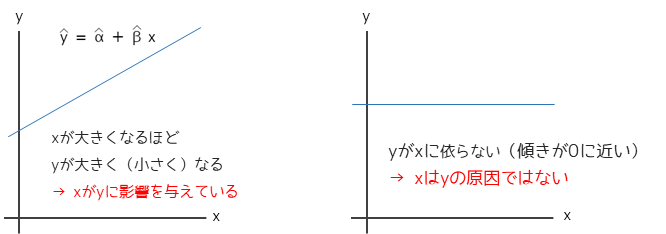
推定された傾きβが統計学的に0と異なるかを判定するために,t検定(仮説検定)を行います.
傾きβに対するt検定の帰無仮説・対立仮説は以下のようになります.
・帰無仮説:傾きβ=0
・対立仮説:傾きβ≠0
検定の結果として有意差がある(p<0.05)場合,傾きβは統計学的に0ではないと判定され説明変数xは目的変数yに影響を与えていると判断することができます.
Excelでは切片αの検定結果も出力されますが,切片αが0であるかは特に意味がないため結果として解釈する必要はありません.
回帰係数の仮説検定を行うためには,誤差εが分布が正規分布である仮定が必要です.サンプルサイズが大きい(n>30)場合は近似的に正規分布に従うため,仮説検定を行うことができます.(中心極限定理)
ここで誤差εとは,回帰式の理論モデルであるy=α+βx+εのうちx以外の要因がyに与える影響を示す誤差項になります.
仮説検定の考え方や手順については,以下のページで解説しています.
残差プロット
残差と推定した回帰式から得られる予測値の散布図を残差プロットと言います.
残差プロットを描くことで,回帰分析に用いたデータや推定した回帰式の問題を見つけることができます.また,回帰係数の仮説検定に必要である残差の正規性についても,残差プロットで判断することができます.
回帰式を用いた予測
回帰式に説明変数xを代入することで,目的変数yを予測することができます.

例えば目的変数yを「年収」,説明変数xを「年齢」として回帰分析を行った場合,求めた回帰式に「年齢」を代入することで「年収」を予測することができます.
説明変数が複数ある場合
説明変数が複数ある場合の回帰分析を重回帰分析と言います.重回帰分析では複数の説明変数を回帰式に含めることで,説明変数ごとの目的変数に対する影響度を比較することができます.
重回帰分析については以下のページで解説しています.
Excelを用いた回帰分析の方法
Excelの用いた単回帰分析の方法を2つ紹介します.Excelを用いた重回帰分析の方法はこちら.
① データ分析ツールを用いた方法
回帰分析を行うツールを選択するために,「データ」タブの「データ分析」をクリックします.

「データ分析」ウィンドウの「回帰分析」をクリックして「OK」を選択します.
「回帰分析」における入力例は以下のようになります.目的変数yを「年収」,説明変数xを「年齢」として回帰分析を行います.
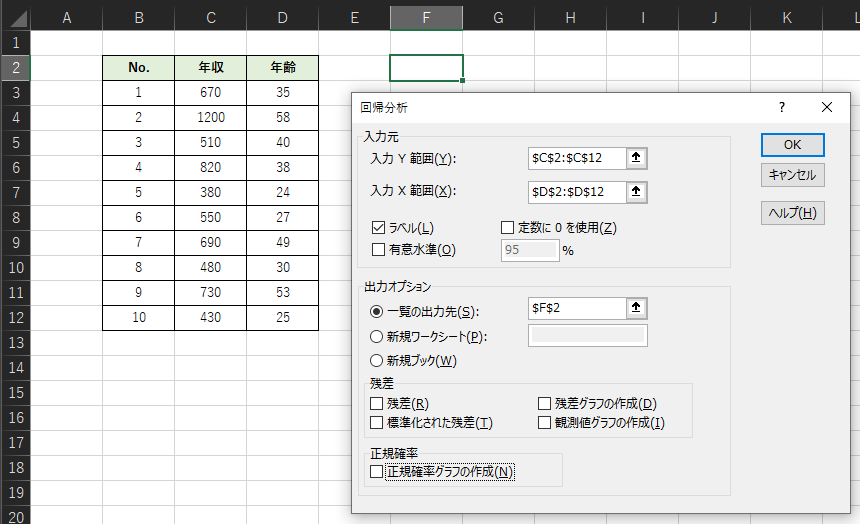
「入力Y範囲」には目的変数yのデータの範囲,「入力X範囲」には説明変数xのデータの範囲を指定します.データの範囲に変数名を含めた場合は,「ラベル」にチェックを入れます.
出力先を指定して「OK」を選択すると,回帰分析の以下のような結果が出力されます.
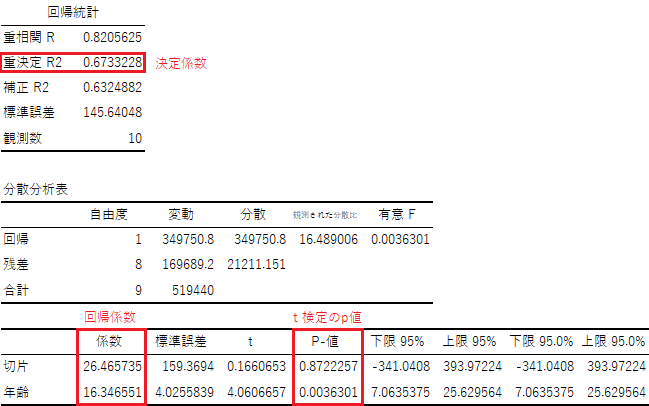
回帰分析における決定係数・回帰係数・t検定のp値が分かります.決定係数はR2=0.673..なので,回帰式の当てはまりは良いと判断できます.説明変数xの回帰係数は16.34..でp<0.05となるので,統計学的に「年齢」は「年収」に影響を与えていると判定されます.※あくまでもサンプルデータです
「t」はt検定の検定統計量,「下限95%」「上限95%」は回帰係数の95%信頼区間の下限値・上限値になります.95%信頼区間とは同じ母集団から100回標本抽出と回帰分析を行ったら,95回はこの範囲に収まることを意味します.「標準誤差」は回帰係数の標準誤差の推定値になります.
② 散布図を用いた方法
対象のデータを選択した状態で,散布図を選択します.
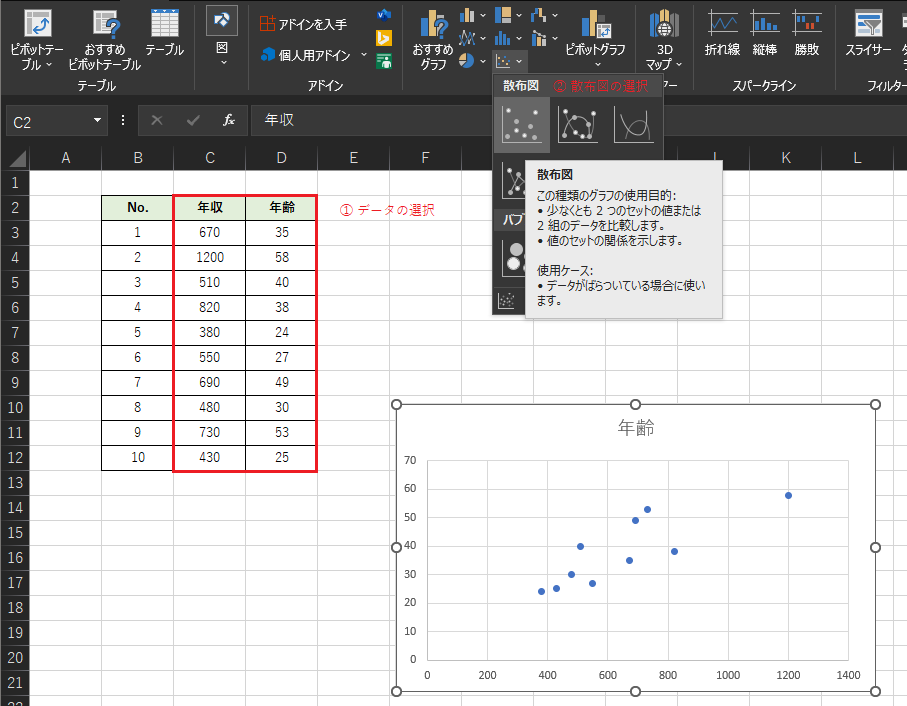
作成した散布図のx軸とy軸の値を確認します.例題では目的変数yを「年収」,説明変数xを「年齢」としたいため作成された散布図のx軸とy軸の値を入れ替える必要があります.
x軸とy軸の値を入れ替えるために,グラフ上で右クリックをして「データの選択」を選択します.(x軸とy軸の値が正しい場合は不要な手順です)
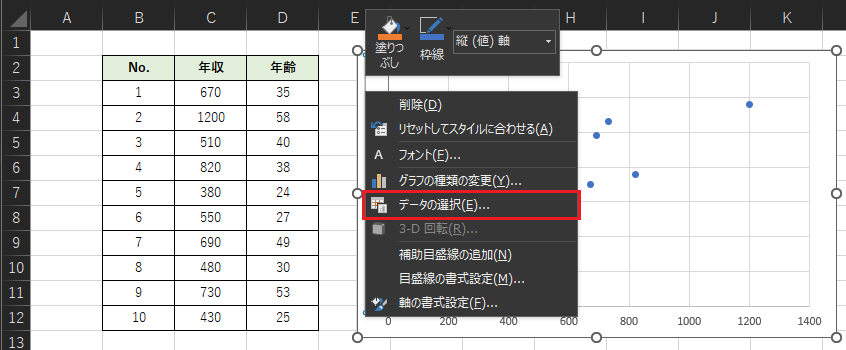
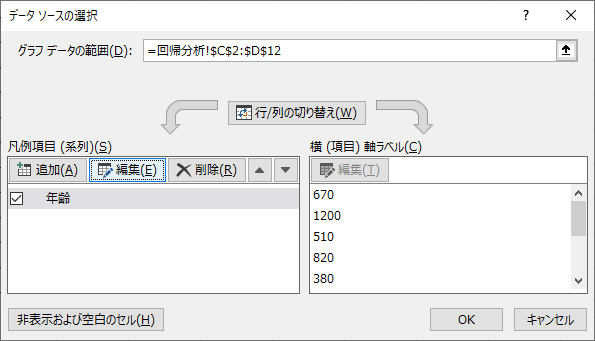
「データソースの選択」ウィンドウの,左側の「編集」を選択します.
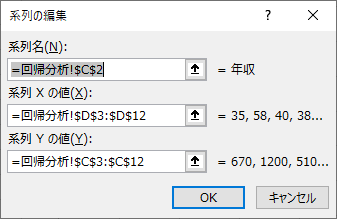
「系列Xの値」「系列Yの値」にそれぞれ設定したいデータの範囲を入力します.入力が完了したら「OK」を選択するとグラフに反映されます.
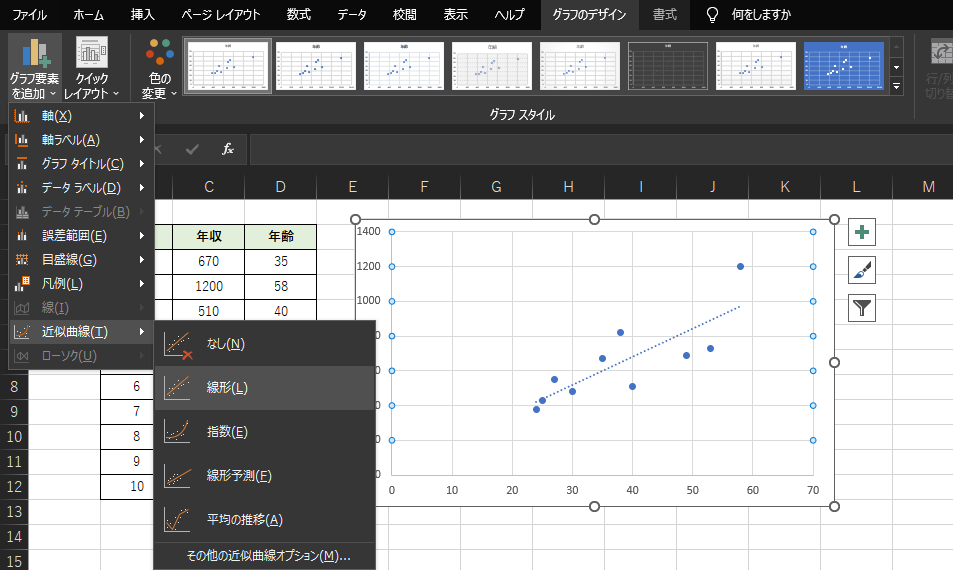
散布図に回帰直線を加えます.「グラフのデザイン」タブ→「グラフ要素の追加」→「近似直線」→「線形」の順に選択すると,散布図上に回帰直線が追加されます.
追加した回帰直線を選択して「書式設定」を行います.最下段にある「グラフに数式を表示する」「グラフにR-2乗値を表示する」を選択すると,散布図上に回帰式と決定係数が表示されます.
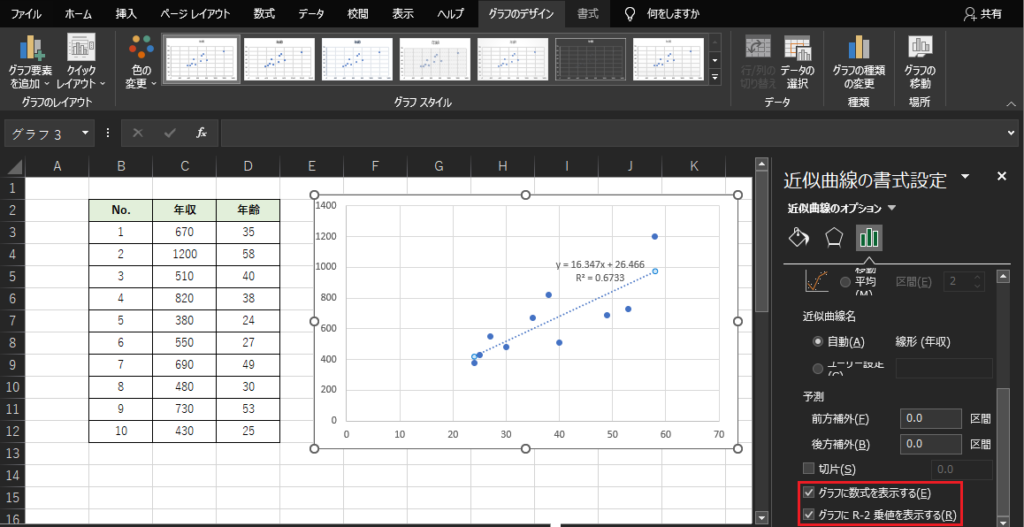
回帰係数と決定係数は①のデータ分析ツールで求めた値と一致しています.