F検定（等分散性の検定）

F検定とは

F検定とは等分散性の検定です．2つの群の母分散が等しいかどうかを判定するために行います．
》 分散とは

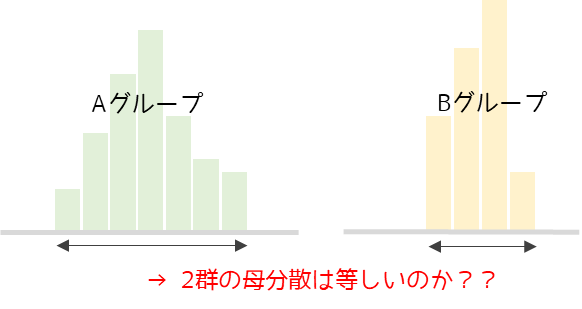
F検定にはF分布という確率分布を用います（帰無仮説が正しい場合，検定統計量はF分布に従うためF検定と呼ばれます）．

以下の図がF検定の考え方になります．

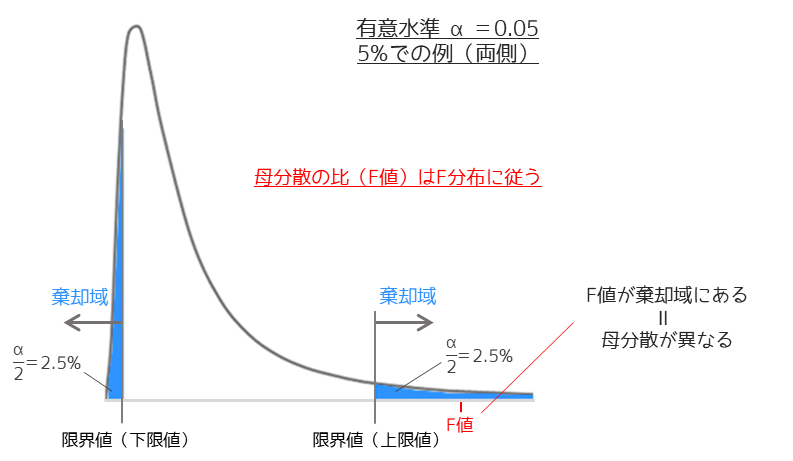
最も重要なのが，2群の母分散の比（F値）はF分布に従うということです．この性質から検定統計量である母分散の比（F値）がF分布の棄却域にあるかどうかで等分散性の検定を行います．

F分布は2群の自由度によって形が変化するため扱うデータに合わせたF分布を用いる必要があります．

F検定はどのような場面で用いるの？という方は補足をお読みください．

F検定の手順

F検定は以下の手順で行います．

① 仮説の設定
　帰無仮説は「2群の母分散に差がない」，対立仮説は「2群の母分散に差がある」として設定します．

② 有意水準の決定
　有意水準α＝0.05または0.01として設定します．一般的にはα＝0.05で設定されます．

③ 検定統計量の算出
　母分散（不偏分散）の比であるF値を検定統計量として求めます．

④ p値の算出
　検定統計量からp値を算出します．Excelではデータから直接p値を求めることができます．

⑤ 有意差判定
　・p値＜有意水準であれば，帰無仮説は棄却されて対立仮説を採択 → 「2群の母分散に差がある」
　・p値\(\geq\)有意水準であれば，帰無仮説は棄却されない → 「2群の母分散に差があるとは言えない」

仮説検定の考え方や用語については，以下のページで解説しています．

》仮説検定とは

例題で用いるデータと仮説の設定

例題では以下のサンプルデータを用います．2つの会社の従業員に対して年収のアンケート調査をした結果になります．

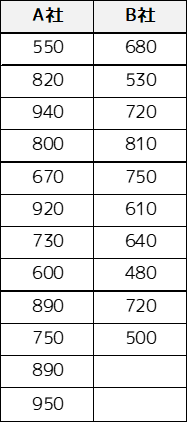
帰無仮説は「2つの会社の年収のばらつき（分散）に差がない」となり，対立仮説は「2つの会社の年収のばらつき（分散）に差がある」と設定します．

有意水準α＝0.05で両側検定を行います．

Excelを用いた計算手順

Excelを用いたp値の計算手順について説明します．

以下のような表を作成して，p値を求めます．

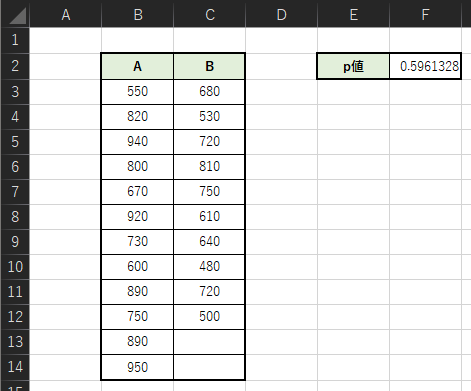
① データを入力する【B列】【C列】
　2群のデータを各1列にデータを入力します．

② p値を求める【F2】
　入力したデータからp値を求めます．F.TEST関数を用いてp値を求めることができます．

　ex) F2の入力式：=F.TEST(B3:B14,C3:C12)

　F.TEST関数は引数として2群のデータ範囲を指定することで，有意水準α＝0.05のp値を返します．

例題ではp値は有意水準以上であるため帰無仮説は棄却されず，「2つの会社の年収のばらつき（分散）に差がないとは言えない」といった結論を得ることができます．

Excelを用いた計算手順（片側検定）

片側検定におけるp値（上側確率）は両側検定のp値を半分にすることで求めることができます．

例題のデータを用いて対立仮説を「A社の年収の分散はB社の年収の分散より大きい」として，片側検定を行なう場合以下の式からp値を求めることができます．

　ex) p値（上側確率）：=F.TEST(B3:B14,C3:C12)/2=0.298..

p値は有意水準以上であるため帰無仮説は棄却されず，「A社の年収の分散はB社の年収の分散より大きいとは言えない」といった結論を得ることができます．

対立仮説を「A社の年収の分散はB社の年収の分散より小さい」とした場合は，p値は下側確率になるので以下のような式を用いる必要があります．

　ex) p値（下側確率）：=1-(F.TEST(B3:B14,C3:C12)/2)

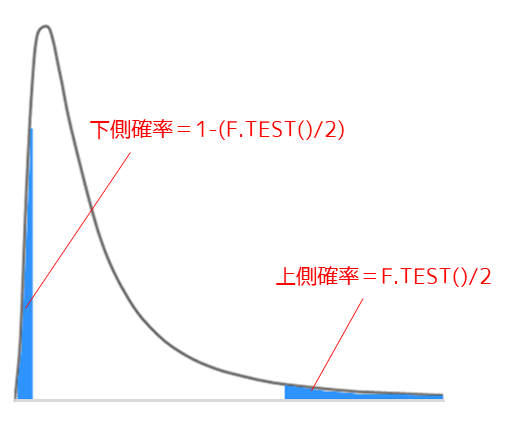
片側検定は仮説の設定段階で，2群の分散のどちらが大きいか（または小さいか）を判断する必要があります．p値を求める式は下側確率と上側確率で異なるため使い分ける必要があります．

検定前に2群の分散の大小を知っている必要があること，p値の求め方が異なることから演習などで片側検定を行う必要がある場合を除いては，両側検定を行うことをおすすめします．

Excelを用いた検定統計量の計算手順

Excelを用いた検定統計量Fの求め方について紹介します．有意差判定を行なうだけであればp値が算出できればよいので検定統計量を求める必要はありません．

検定統計量は以下のような表を作成して求めます．

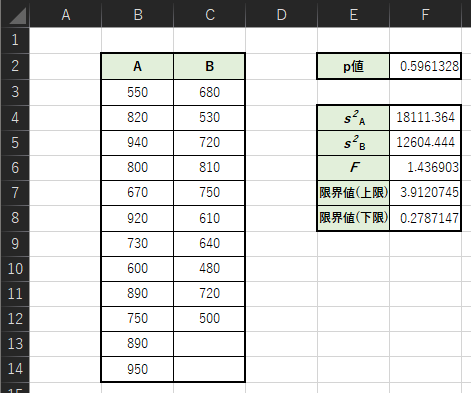
① 不偏分散を求める【F4】【F5】
　2群の不偏分散s²を求めます．不偏分散は標本分散の期待値が母分散に一致するように標本分散にn/(n-1)をかけた値になります．（nはサンプルサイズ）

　Excelでは不偏分散はVAR.S関数で求めることができます．

　ex) F4セルの入力式：=VAR.S(B3:B14)

② 検定統計量Fを求める【F6】
　検定統計量Fは不偏分散の比であるので以下の式で求めることができます．

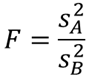
　s²は①で求めた不偏分散です．

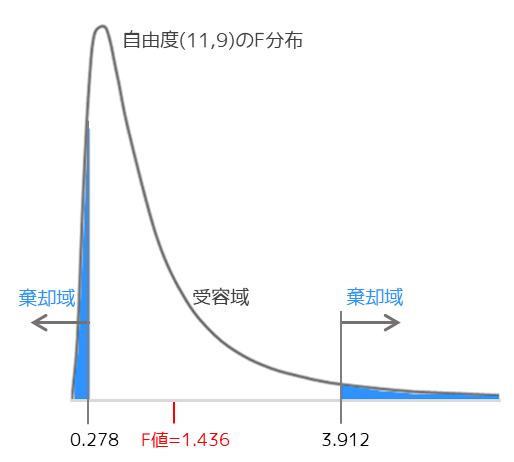
例題では，検定統計量Fは1.4369…となります．検定統計量を用いて有意差判定を行なう場合は，F分布表から限界値を読み取り大小を比較します．（F分布表の読み方については割愛します）

参考までにExcelではFINV関数を用いて，有意水準と自由度から限界値を求めることができます．例題では有意水準α＝0.05の両側検定で，自由度f₁=11，f₂=9となるので以下の式で求めることができます．
※ 自由度はサンプルサイズ－1で求めることができます．

　・限界値（上限）：=FINV(0.025,11,9)　【F7】
　・限界値（下限）：=FINV(1-0.025,11,9)　【F8】

上限値は3.912..，下限値は0.278..となり検定統計量は受容域にあるため帰無仮説は棄却されません．

補足 F検定は必要なのか？

F検定は対応のないｔ検定の事前検定として行なうことが多いです．対応のないｔ検定の前提条件として，2標本の母分散が正規分布に従うと仮定できることと，等分性があるためです．正規性についてはF検定の前提条件でもあります．

F検定を行い帰無仮説が棄却された場合（母分散に差がある場合）は，ウェルチのｔ検定を行います．

しかしながら，近年はF検定を事前に行なうことで多重性の問題（検定の繰り返すことで第一種の過誤を犯す可能性が上がること）が発生するため，等分散性に疑いがある場合はF検定を行わずに直接ウェルチのｔ検定を行なうことが多いです．

つまり，F検定を実践で使う場面はほとんど無いのが現実です．．

》対応のないｔ検定
》ウェルチのｔ検定