エラーバーとは
エラーバーとはデータのばらつきを示す棒状のグラフになります.以下の図のように,棒グラフの上部に付けて図示することが多いです.
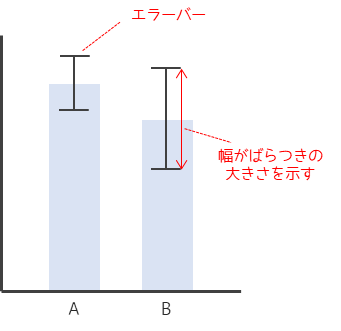
エラーバーは幅が大きいほど,ばらつきが大きいことを示します.図中のエラーバーではデータAより,データBの方がばらつきが大きいことを示しています.
エラーバーの種類
エラーバーには,以下の3つの種類があります.
① 標準偏差(SD)
② 標準誤差(SE)
③ 95%信頼区間
それぞれのエラーバーの見方や意味について説明します.
① 標準偏差のエラーバー
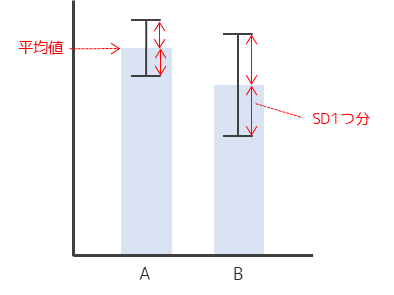
標準偏差のエラーバーでは平均値±標準偏差を表します.棒グラフの上端である平均値から,エラーバーの上端・下端までの長さが標準偏差1つ分を意味します.
標準偏差はデータのばらつきを示す統計量なので,エラーバーの長さが長いほど標本のばらつきが大きいということを意味します.
② 標準誤差のエラーバー
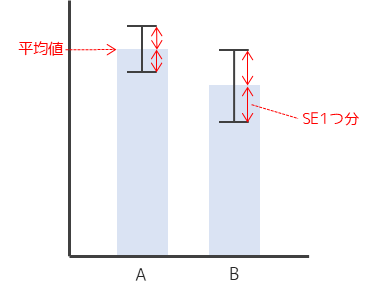
標準誤差のエラーバーでは平均値±標準誤差を表します.棒グラフの上端である平均値から,エラーバーの上端・下端までの長さが標準誤差1つ分を意味します.
標準偏差は標本分布のばらつきを示す統計量なので,エラーバーの長さが長いほど標本平均のばらつきが大きい=推定した母平均の精度が低いということを意味します.標準誤差は標準偏差をサンプルサイズの平方根で割ることで求めることができます
平均値の差を比較する仮説検定の結果としては,推定した母平均の精度を示すために標準誤差のエラーバーを用いるのが一般的です.
③ 95%信頼区間のエラーバー
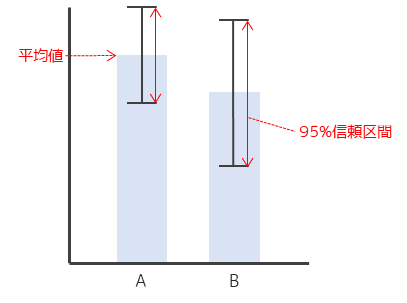
95%信頼区間のエラーバーでは母平均の95%信頼区間を表します.エラーバーの上端から下端までの長さが95%信頼区間を意味します.
標本平均が標準化正規分布に従う(n=30以上)場合,95%信頼区間は標本平均±1.96×標準誤差で求めることができます(中心極限定理).
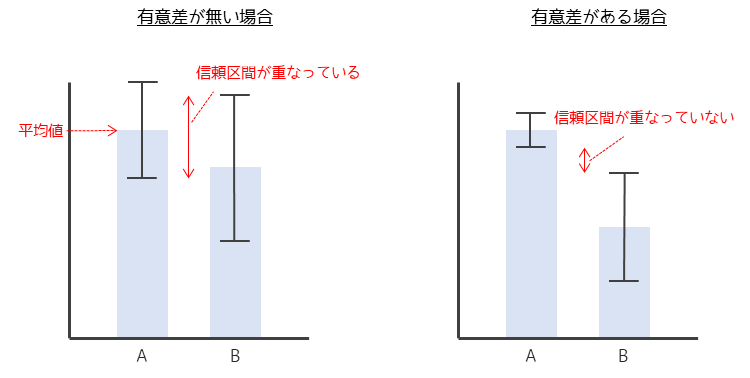
信頼区間のエラーバーは統計的な有意差を示すことができます.母平均の検定では,エラーバーが重なっている場合は有意差なし,重なっていない場合は有意差ありと判断することができます.
StaatAppを用いてエラーバーを作成する
統計解析アプリStaatAppではExcelを用いた方法よりも簡単に,エラーバーを作成することができます.無料版機能で仮説検定やエラーバー作成を実行できるので,お気軽にダウンロードしてお使いください.
》統計解析アプリStaatApp
》StaatAppで作成するエラーバー
Excelを用いたエラーバーの作り方
Excelを用いたエラーバーの作り方について紹介します.
例題として副業をしている社会人と副業をしていない社会人,各10人の年収を比較します.エラーバーを作成するために以下のようなデータを準備します.※ 恣意的なサンプルデータです.
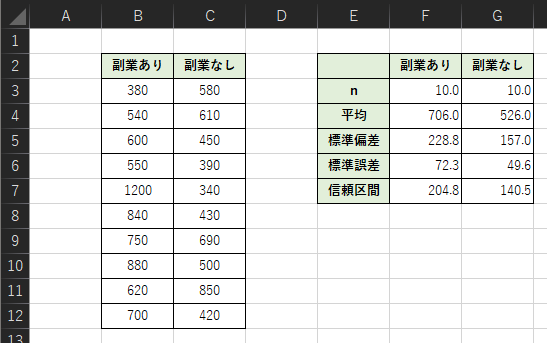
入力した計算式は以下のようになります.
・F4セル:=AVERAGE(B3:B12)
・F5セル:=STDEV.S(B3:B12)
・F6セル:=F5/SQRT(F3)
・F7セル:=T.INV.2T(0.025,F3-1)*F5/SQRT(F3-1)
※ t分布を用いた95%信頼区間の平均値から端までの長さになります.
エラーバーを作成する手順を説明します.
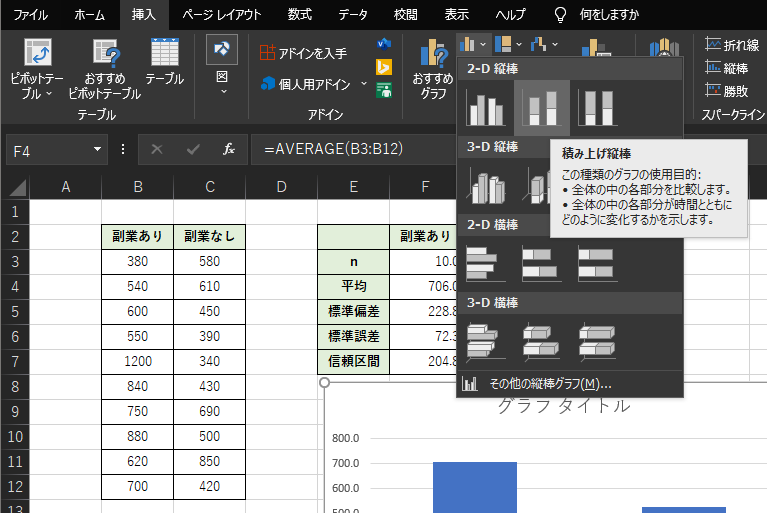
① 棒グラフの作成
平均値を入力したセルを選択した状態で,棒グラフの作成を行います.
「挿入」タブの「積み上げ縦棒」を選択することで,平均値を示した2つの棒グラフが作成されます.
② エラーバーの作成
作成した棒グラフにエラーバーを追加します.
画面左上の「グラフ要素の追加」から,「誤差範囲」→「その他の誤差範囲オプション(M)」を選択します.
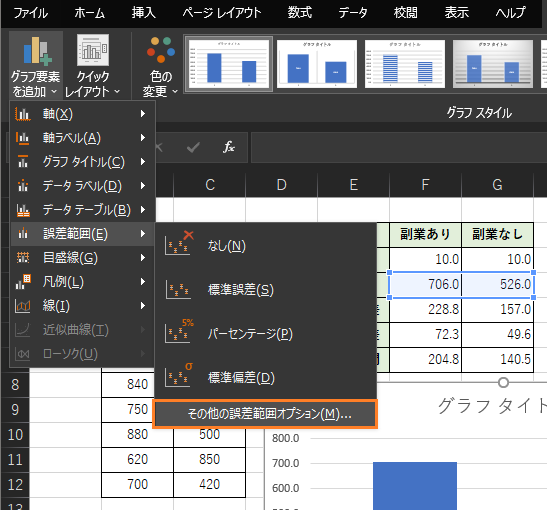
画面右側に「誤差範囲の書式設定」が表示されるので,「誤差範囲」項目から「ユーザー設定(C)」を選択して「値の指定(V)」をクリックします.
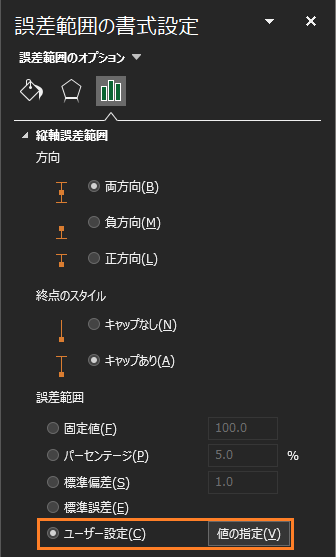
「ユーザー設定の誤差範囲」というウインドウが表示されるので,「正の誤差の値(P)」と「負の誤差の値(N)」に表示したいエラーバーの値が入力されたセルを選択します.例では,標準誤差を表示します.
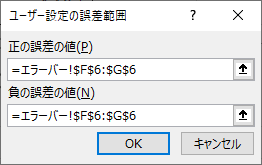
「OK」を選択すると,棒グラフにエラーバーが表示されます.
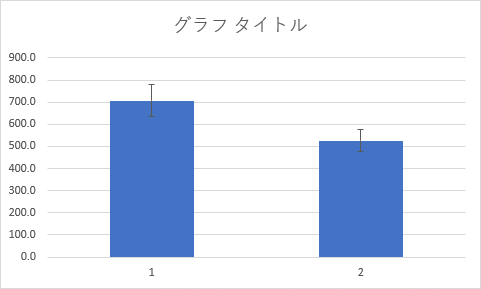
以上がエラーバーの作成方法になります.あとは見やすいように棒グラフの色の調整などを行ってください.
仮説検定の結果の示し方
t検定などの仮説検定の結果を示すために,エラーバーを用いることがあります.
仮説検定の結果を示す場合は,グラフのキャプションにエラーバーが何を示しているのかとサンプルサイズを記述します.(ほとんどの場合,標準誤差を示します.)
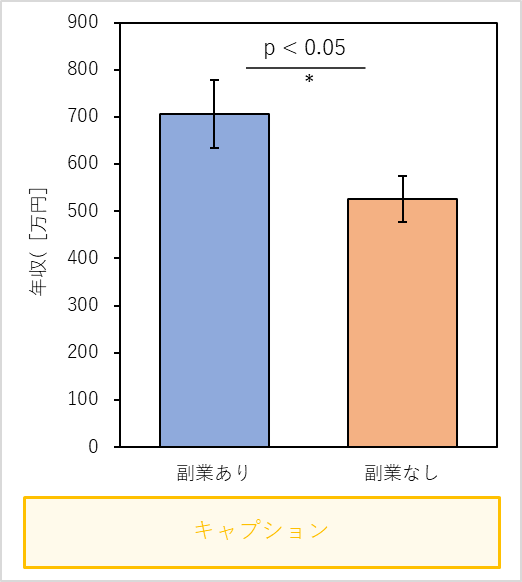
検定結果として有意差がある場合は,グラフ内にp値を記述することが多いです.
因みに上記のグラフは,世界的に有名な科学ジャーナル”Nature”で使われているようなグラフデザインになります.(p値の表示以外はExcelで作図しています.)
グラフや表では有意差を示す際に,*(アスタリスク)を使用するのが一般的です.*の数によって以下のような意味を持ちます.
* :p<0.05
** :p<0.01
*** :p<0.001
有意差がない場合は,N.S.(non-significant)と表記することもあります.
仮説検定やp値については以下のページで解説しています.
統計解析に用いる可視化手法
統計解析ではエラーバー以外にもデータの分布を調べる・示すためにグラフがよく用いられます.代表的なデータの分布を表すグラフとしてヒストグラム(度数分布図)や散布図があります.
グラフを用いることでデータの傾向を視覚的に捉えることができます.また,統計解析の元データを効率的に示すことができます.
グラフの選び方
統計解析においてグラフは様々な種類があります.分析対象のデータ・分析の目的に対して最適なグラフの選び方について,以下のページで解説しています.










