バートレット検定

バートレット検定とは

バートレット検定とは3群以上の等分散性の検定です．3つ以上のグループの母分散が等しいかどうかを判定するために行います．

》分散とは

バートレット検定は主に分散分析の事前検定として行われます．詳しくは補足①まで．

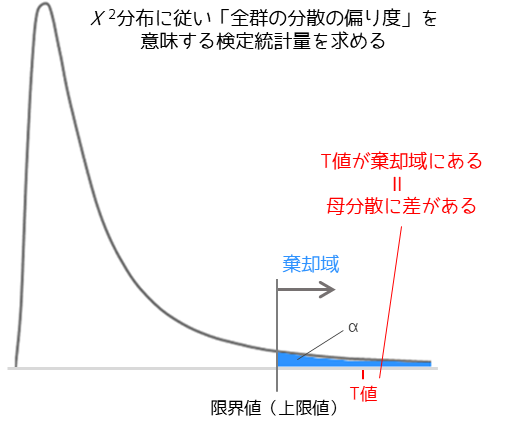
バートレット検定では比較する全群の分散の偏り度を表す検定統計量を求めます．検定統計量はΧ²乗分布に従い，検定統計量が限界値より大きい場合に帰無仮説は棄却され，母分散に差があるといった結論を得ることができます．

Χ²分布は自由度によって形が変化するため，扱うデータに合わせたΧ²分布を用いる必要があります．

バートレット検定の手順

バートレット検定は以下の手順で行います．

① 仮説の設定
　帰無仮説は「3群以上の母分散に差がない」，対立仮説は「3群以上の母分散に差がある」として設定します．

② 有意水準の決定
　有意水準α＝0.05または0.01として設定します．一般的にはα＝0.05で設定されます．

③ 検定統計量の算出
　全群の分散の偏り度であるT値を検定統計量として求めます．

④ p値の算出
　検定統計量からp値を算出します．

⑤ 有意差判定
　・p値＜有意水準であれば，帰無仮説は棄却されて対立仮説を採択 → 「3群以上の母分散に差がある」
　・p値\(\geq\)有意水準であれば，帰無仮説は棄却されない → 「3群以上の母分散に差があるとは言えない」

仮説検定自体の考え方や用語については，以下のページで解説しています．

》仮説検定とは

検定結果を間違いたくない方へ

Excelを用いた計算方法より簡単・正確に，バートレット検定の検定結果を調べることができる統計解析アプリStaatAppを販売しております．

StaatAppではバートレット検定以外にも様々な仮説検定をマウス操作だけで実行することができます．詳細は以下のページをお読みください．

》StaatAppで行う仮説検定
》統計解析アプリStaatAppとは

例題で用いるデータと仮説の設定

例題では以下のサンプルデータを用います．4つの業界の会社員に対して年収を調査した結果になります．

帰無仮説は「4つの業界の年収のばらつき（分散）に差がない」となり，対立仮説は「4つの業界の年収のばらつき（分散）に差がある」と設定します．

有意水準α＝0.05で両側検定を行います．

Excelを用いた計算手順

Excelを用いたp値の計算手順について説明します．

以下のような表を作成して，p値を求めます．

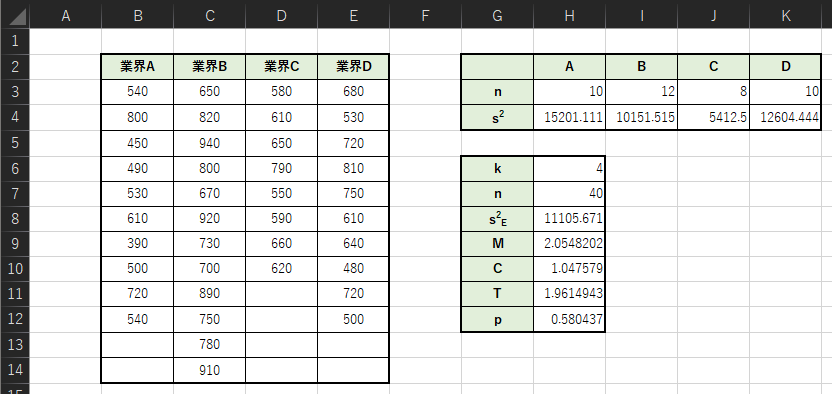
各セルの入力式は以下のようになります．
　・H3：=COUNT(B3:B14)
　・H4：=VAR.S(B3:B14)
　・H7：=COUNT(B3:E14)
　・H8：=((H3-1)*H4+(I3-1)*I4+(J3-1)*J4+(K3-1)*K4)/(H7-H6)
　・H9：=(H7-H6)*LN(H8)-((H3-1)*LN(H4)+(I3-1)*LN(I4)+(J3-1)*LN(J4)+(K3-1)*LN(K4))
　・H10：=1+(1/(3*(H6-1)))*(1/(H3-1)+1/(I3-1)+1/(J3-1)+1/(K3-1)-1/(H7-H6))
　・H11：=H9/H10
　・H12：=CHIDIST(H11,H6-1)

計算手順について解説します．

① データを入力する【B-E列】
　4群のデータを各1列にデータを入力します．

② 各群のサンプルサイズを求める【H-K3】
　入力した各群のサンプルサイズを計算します．Excelではデータが入力されているセルを選択して，データの個数を表示させることでサンプルサイズを求めることができます．

　表ではCOUNT関数を用いて計算しています．

③ 各群の不偏分散を求める【H-K4】
　各群の不偏分散を求めます．ExcelではVAR.S関数を用いて計算することができます．

④ 群数・全群のサンプルサイズを求める【H6】【H7】
　比較する群数と全群のサンプルサイズを求めます．サンプルサイズは②と同様の方法で求めることができます．

⑤ 分散の偏り度を求める【H8-9】
　分散の偏り度Mを求めます．分散の偏り度を以下の式で求めることができます．

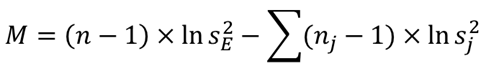
　n_jは群jのデータ数，s_j²は群jの不偏分散になります．s_E²は郡内変動を表す分散で以下の式で求めることができます．

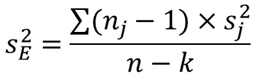
⑥ 偏り度の補正係数Cを求める【H10】
　データ数が増加すると偏り度が大きくなるため，補正するための補正係数を求めます．補正係数Cは以下の式で求めることができます．

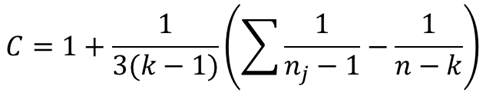
⑦ 検定統計量Tを求める【H11】
　⑤と⑥で求めた値から検定統計量Tを算出します．検定統計量は以下の式で求めることができます．

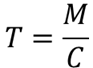
⑧ p値を求める【H12】
　検定統計量からp値を求めます．ExcelではCHIDIST関数を用いて求めることができます．CHIDIST関数の引数は以下になります．

　CHIDIST関数の引数：CHIDIST(“検定統計量”,”自由度”)

　自由度は群数－1で求めることができます．

例題ではp値は有意水準以上であるため帰無仮説は棄却されず，「4つの業界の年収のばらつき（分散）に差がないとは言えない」といった結論を得ることができます．

》正しく理解したい！p値とは

補足① 分散分析との関係

バートレット検定は分散分析の事前検定として行なうことが多いです．分散分析の前提条件として，2標本の母分散が正規分布に従うと仮定できることと，等分性があるためです．正規性についてはF検定の前提条件でもあります．

バートレット検定を行い帰無仮説が棄却された場合（母分散に差がある場合）は，3群以上のウェルチの検定やクラスカス・ウォリス検定を行います．

》分散分析
》クラスカル・ウォリス検定

補足② 扱うデータの前提条件

バートレット検定は扱うデータの母集団は正規分布に従う必要があります．正規分布に従わない場合は，非正規性を比較するルビーン検定を行います．

》正規性の調べ方

補足③ Pythonを用いた計算手順

Pythonを用いたp値の計算方法について，サンプルコードは以下になります．

from scipy import stats

A = [540, 800, 450, 490, 530, 610, 390, 500, 720, 540]
B = [650, 820, 940, 800, 670, 920, 730, 700, 890, 750, 780, 910]
C = [580, 610, 650, 790, 550, 590, 660, 620]
D = [680, 530, 720, 810, 750, 610, 640, 480, 720, 500]

result = stats.bartlett(A, B, C, D)
print(result)

==> 実行結果
BartlettResult(statistic=1.9614943103119309, pvalue=0.5804370445563012)

PythonではScipyライブラリを用いてp値を計算することができます．

出力結果はpvalue＝0.580437..となっており，Excelでの計算結果と一致することがわかります．