ボンフェローニ補正(Bonferroni補正)とは
ボンフェローニ補正とは様々なデータに対して用いることができる,万能な多重比較になります.扱うデータが正規分布に従わない場合や対応のない場合,対応のある場合のいずれのう場合でも用いることができます.
比較方法としては全ての2群ごとに検定を行い,有意水準を検定回数で割った値を新しい有意水準とする単純な方法となります.
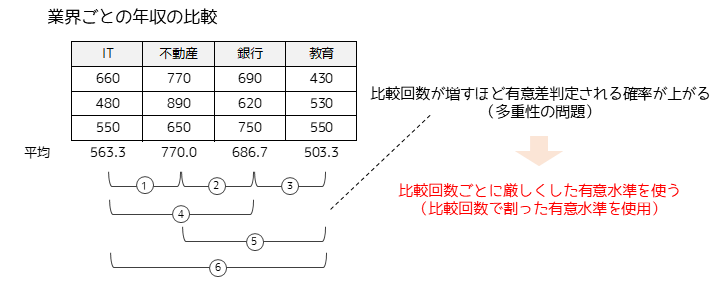
ボンフェローニ補正の欠点としては,比較する群数が多くなった際に有意差が出にくくなることです.目安として5群以上の検定を行う場合に検出力が下がります(有意差が出にくくなります).
多群に対して検定を行なう場合は,テューキー法など別の多重比較が望ましいです.
➔ ボンフェローニ補正以外の多重比較・多重比較の考え方について
ボンフェローニ補正の手順
ボンフェローニ補正は以下の手順で行います.
① 仮説の設定
帰無仮説は「各群間に差がない」,対立仮説は「各群間に差がある」として設定します.正確には2群の比較を行なう検定方法によって仮説は異なります.t検定を行なう場合,帰無仮説は「各群の母平均に差がない」となります.
② 有意水準の決定
有意水準α=0.05または0.01とします.一般的には0.05で設定されます.ボンフェローニ補正は両側検定のみとなります.
③ p値の算出
扱うデータに合わせた2群の検定を行い,p値を求めます.
④ 有意水準の補正
②で設定した有意水準を③の検定回数で割って補正します.
⑤ 有意差判定
補正後有意水準>p値であれば,帰無仮説は棄却されて対立仮説を採択 → 「比較した2群に差がある」
補正後有意水準\(\leq\)p値であれば,帰無仮説は棄却されない → 「比較した2群に差があるとは言えない」
仮説検定の考え方や用語については,以下のページで解説しています.
StaatAppを用いたボンフェローニ補正
統計解析アプリStaatAppではボンフェローニ補正を,マウス操作だけで簡単に実行することができます.ボンフェローニ補正に加えてシダック法やホルム法,テューキー・クレーマー法など様々な多重比較を実行可能です.
詳細は以下のページをご覧ください.
》統計解析アプリStaatApp
》StaatAppを用いたボンフェローニ補正
例題で用いるデータと仮説の設定
例題では以下のサンプルデータを用います.4つの業界で働いている社会人に対して年収を調査した結果になります.
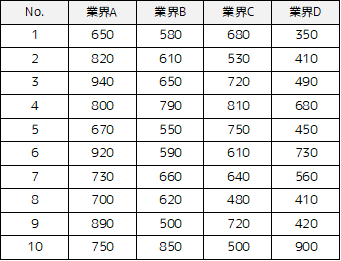
帰無仮説は「各業界ごとに年収の差はない」となり,対立仮説は「比較した業界間で年収に差がある」と設定します.
有意水準α=0.05で検定は行います.
Excelを用いた計算手順
Excelを用いたボンフォローニ補正を行う方法を説明します.
シートの作成例は以下のようになります.
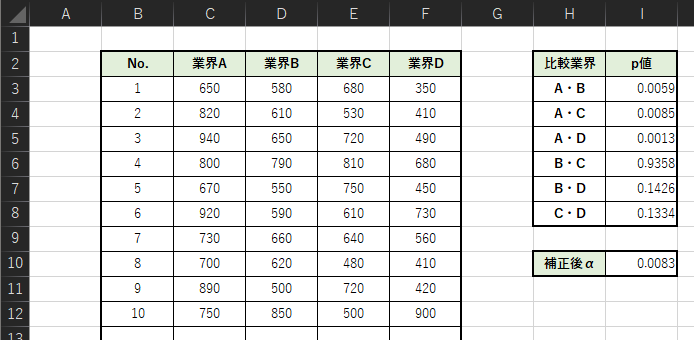
I列とJ列は以下のようになります.
・I3-8:対応のないt検定のp値
・I10:(有意水準α=0.05)/(組み合わせ数=6)
詳細な手順と用いた数式について解説します.
① 2群ごとに検定を行いp値を求める
2つのグループごとに検定を行いp値を求めます.
例題では2群の検定方法として対応のないt検定を行いp値を求めています.
② ボンフェローニ補正を行う
有意水準に対して2群ごとの組み合わせ数(①での検定回数)を割ることで補正後有意水準を求めます.
例題では組み合わせ数は6だったので,有意水準α=0.05/6=0.0083..となります.
③ 補正値から有意差の判定をする
①で求めたp値と補正後有意水準を比較します.p値が補正後有意水準より小さい場合,帰無仮説は棄却され対立仮説が採択されます.
例題では業界Aと業界Bの検定において,p値が0.0059..となっており補正後有意水準より小さいため,帰無仮説は棄却され対立仮説が採択されます.よって,「業界Aと業界Bの社会人の年収には差がある」といった結論が得られます.
加えて業界Aと地域Dにおいても,社会人の年収に差があるといったことが分かります.
以上が,Excelで行うボンフォローニ補正の計算手順になります.
補足① ボンフェローニ補正とは(詳細版)
ボンフェローニの補正についてより詳しく解説します.
ボンフェローニ補正とは,多重性の問題を解決するために意図的に有意水準低くする手法です.有意水準を低くするための補正方法として”各グループ間の比較回数で割る”と定めた手法がボンフェローニ補正となります.

ボンフェローニ補正自体は,有意水準を各グループ間の比較回数で割るといった操作しか行いません.したがって,検定全体としては2群の比較においてp値を求める手法選択や計算過程の方が難しいかつ重要です.
2群の検定方法は以下のページで紹介しています.
また,有意水準の補正方法の違いによって様々な多重比較の方法があります.ボンフェローニ補正に類似する手法については補足②で紹介します.
補足② ボンフェローニ補正の類似手法
ボンフェローニ補正のように,有意水準を補正する多重比較について3つ紹介します.
① シダック(サイダック・Sidak)補正
ボンフェローニ補正と比較して有意差が出やすい手法です.有意水準の補正方法は以下の式を用います.
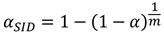
ここで,αは有意水準,mは2群の比較回数になります.例題のように,有意水準α=0.05で組み合わせ数が6の場合,補正後有意水準は0.0085..となりボンフェローニ補正で求めた0.0083より有意水準が大きいことが分かります.
② ホルム(Holm)法
ホルム法もボンフェローニ補正と比較して有意差が出やすい手法です.ホルム法はp値ごとに有意水準を補正するため手順としては少し複雑になります.有意水準の補正とp値の比較手順は以下になります.
(1) 2群の比較回数をNとして,検定で求めたp値を小さい順に並べます.
(2) 最も小さいp値に対して,補正後有意水準をα/Nとして比較します.
「p値\(\geq\)α/N」の場合,帰無仮説を棄却して対立仮説を採択します(p値に該当する群間に有意差があると判断します).
「p値>α/N」の場合,帰無仮説は棄却されず検定終了です.
(3) (2)で有意差が合った場合,2番目に小さいp値に対して,補正後有意水準をα/(N-1)として比較
します.
「p値\(\geq\)α/(N-1)」の場合,帰無仮説を棄却して対立仮説を採択します(p値に該当す
る群間に有意差があると判断します).
「p値>α/(N-1)」の場合,帰無仮説は棄却されず検定終了です.
(4) 有意差が出たら,k番目に小さいp値と補正後有意水準をα/(N+1-k)として有意差が出なくなるまで比較を行います.
③ ライアン(Ryan)法
ライアン法はボンフェローニ補正より有意差が出やすくホルム法よりも若干厳しい手法になります.有意水準の補正ではp値ごとに以下の式を用います.
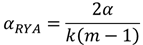
ここで,αは全体の有意水準, kは群数,mは全群を平均値順に並べた際に比較する群間にある群数+1になります.例題ではグループの平均順は地域A>C>B>Dとなり,地域Aと地域Dの比較に用いる補正式中のm=3で,補正後有意水準=2×0.05/(4×2)=0.0125となります.










