生存時間データに対する多変量解析である,Cox比例ハザード回帰について解説します.
考え方の基本から具体例,Pythonを用いた計算方法まで紹介しています.
Cox比例ハザード回帰とは
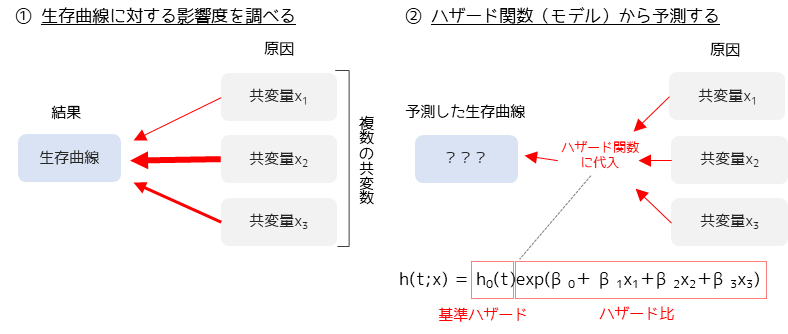
Cox比例ハザード回帰とは,生存時間データのための重回帰分析です.生存時間データは生存曲線で表され,イベント発生までの時間を示すデータになります.Cox比例ハザード回帰を行うことで,生存時間データに影響を与えている要因(共変量)を調べることや生存曲線を予測するモデルを作ることができます.
ハザードとは時刻tまで生存してるが,その直後に死んでしまう確率つまり時間tでの死亡確率になります.
Cox比例ハザード回帰ではカプラン・マイヤー法と同様に,解析時点でイベントが発生していない打ち切りデータを扱うことができます.
ハザード比とは
Cox比例ハザード回帰では生存時間データに対する影響度を調べるために,ハザード比を計算します.
ハザード比とはある共変量xiが”1”でその他の共変量が”0”の場合の,ハザードと基準ハザードh0(t)の比になります.基準ハザードh0(t)は全ての共変量が”0”の場合のハザードで,時間経過のみに依存します.
ハザード比が1より大きい場合は,その共変量xiはイベントの発生確率を上昇させることを意味します.1より小さい場合は,発生確率を減少させることを意味します.
比例ハザード性
Cox比例ハザード回帰の前提条件として,比例ハザード性を満たす必要があります.
比例ハザード性とは2群間のハザード比(生存率の比)がどの時間においても一定であることです.生存曲線においては,以下の図のようにどの時点においても生存率の比が一定であれば比例ハザード性があると言えます.
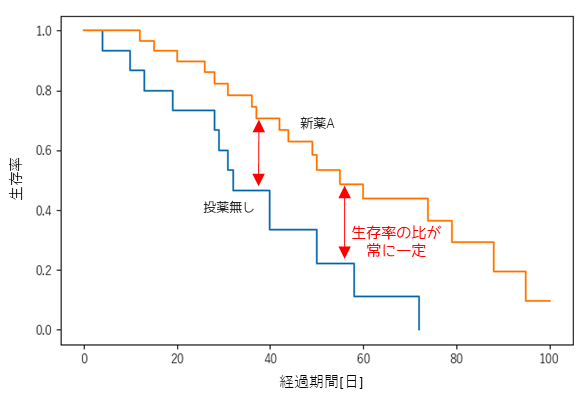
時間が経過するごとにハザード比が変化する場合は,層別Cox比例ハザードモデルや時間依存型共変量を採用するなどの対処方法があります.
具体例と結果の見方
Cox比例ハザード回帰を例題を用いて具体的に説明します.
生存時間データにおけるイベントを「副業としてのブログ運営をやめる」と設定して,運営者の属性がブログ運営にどのように影響を与えているかを,Cox比例ハザード回帰を用いて分析します.
サンプルデータは以下のようになります.イベントの発生=ブログ運営をやめる,としてデータを作成しています.

実際に計算を行う際は,イベントや年齢などのカテゴリーデータをダミー変数に変換する必要があります.
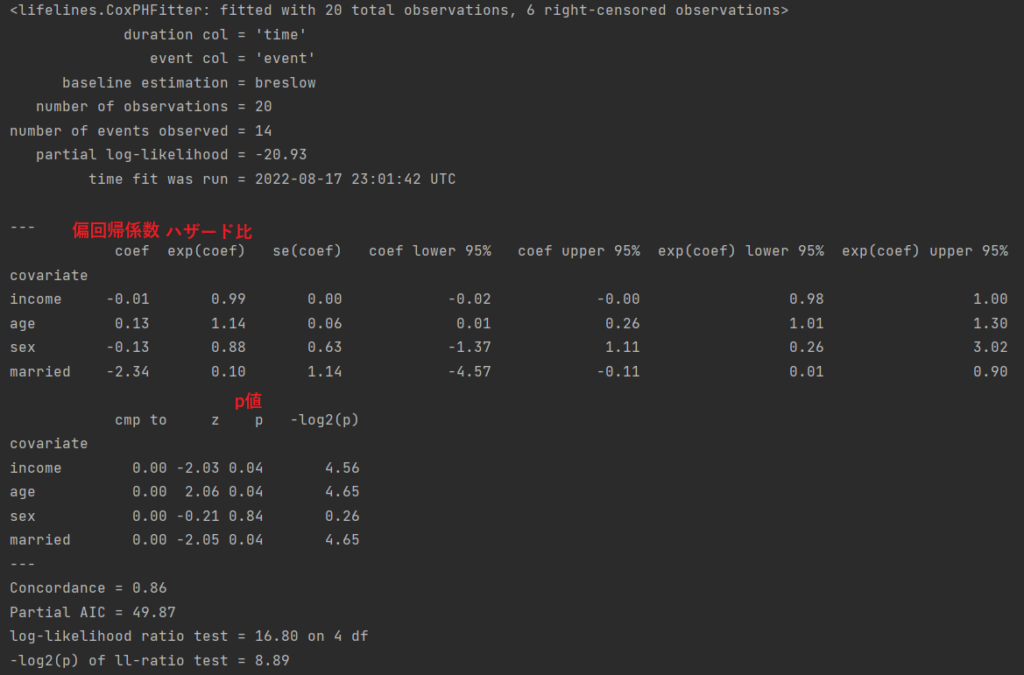
解析結果は以下のように出力されます.
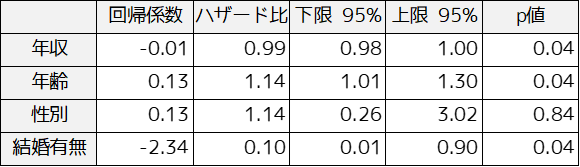
Cox比例ハザード回帰分析の結果おいて,特に見るべき項目はハザード比とp値になります.
ハザード比は既に説明したように,共変量がどのようにハザード関数に影響を与えているかを示します.「結婚有無」は値が非常に小さいため,結婚している(結婚=1に変換)ほどイベントが発生しにくい,つまりブログ運営を比較的長く続けるということがわかります.「性別」では1よりわずかに大きいため,男性(男性=1)の方が女性よりブログ運営をやめる傾向が若干あるということがわかります.
p値では回帰係数が統計学的に有意であるかを示します.ある共変数がp<0.05の場合,統計学的に有意であるつまりその共変数の変動がハザード関数の変動に影響を与えていると判定することができます.「年収」「年齢」「結婚有無」ではp<0.05であるため,統計学的に有意であると判定できます.「性別」は有意差がないため共変量として統計学的に意味がないと判断することができます.
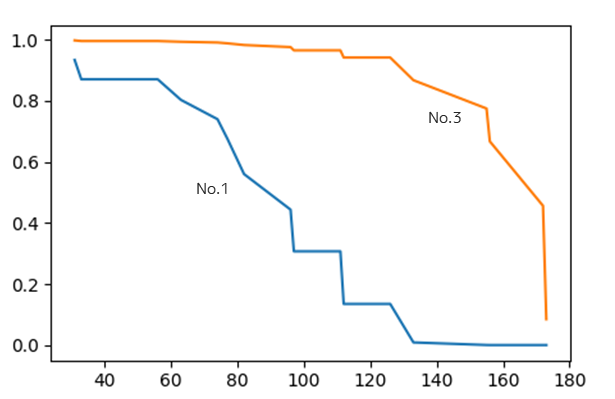
作成したハザード関数を用いて生存曲線の予測を行うことも可能です.No.1とNo.3の方の予測した生存曲線は以下のようになります.
解析ソフトによっては比例ハザード性の検定を行うことも可能です.比例ハザード性の検定は帰無仮説を「比例ハザード性が満たされている」として共変量ごとに行います.

上記のような結果となった場合,全ての共変量でp値>0.05なので有意差はなく帰無仮説は棄却されません.よって明らかに比例ハザード性に違反していることはないと考えることができます.
Concordance index(C-index, C統計量)
C-indexは,生存時間予測モデルの性能を評価するための指標の1つです.特に,モデルが予測するリスクスコアのランキングが,観察される生存時間とどれだけ一致しているかを示す指標として使用されます.
C-indexの値は0から1までの範囲をとります.C-indexが0.5の場合,モデルの予測はランダムな予測と同等であり,1に近いほどモデルの予測が正確であることを示しています.あくまでも目安としてですが,0.8以上であれば比較的モデルの性能が良いと判断されることが多いです.
ロジスティック回帰分析のような二項分類問題では,C-indexのような指標値をAUC(Area Under the ROC Curve)と表現します.
Cox比例ハザード回帰の実行方法
Cox比例ハザード回帰は複雑な計算が必要なため,手計算やExcelを用いて行うことは難しいです.一般的にはRやPython,有料統計解析ソフトを用いて実行されます.
本サイトでは下記Pythonを用いた方法に加えて,StaatAppを用いた方法を紹介しています.StaatAppとは任意のデータをマウス操作だけで統計解析ができるPC用アプリです.
初めての方はほぼ全ての機能を無料で利用できるので,お気軽にダウンロードしてお使いください!
》StaatAppで行うCox比例ハザード回帰
》統計解析アプリStaatAppとは
Pythonを用いた計算方法
Pythonを用いたCox比例ハザード回帰を紹介します.
例題と同様のサンプルデータをCSVファイルとして作成して用います.
# ライブラリのインポート
import pandas as pd
# データの読み込み
df_workers = pd.read_csv("cox.csv")
print(df_workers.head())
No. time event income age sex married
0 1 31 1 580 32 1 0
1 2 97 1 430 28 0 0
2 3 126 0 800 45 1 1
3 4 56 0 780 36 0 0
4 5 172 1 690 42 0 1Cox比例ハザード回帰は生存時間解析を行うライブラリであるlifelinesを用いて行います.以下のように記述することで実行可能です.
# ライブラリのインポート
from lifelines import CoxPHFitter
# Cox比例ハザード回帰の実行
cph = CoxPHFitter()
cph.fit(df_workers.iloc[:, 1:7], duration_col="time", event_col="event")
cph.print_summary()実行結果は以下のように出力されます.
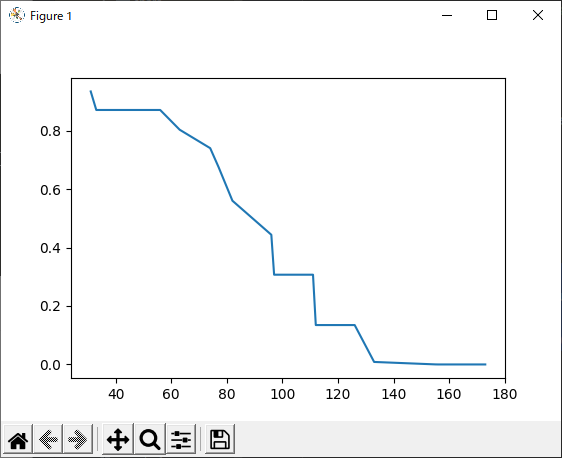
作成したハザード関数を用いてNo.1の方の生存曲線の予測を行います.Matplotlibを用いて生存曲線を描画します.
# 予測した生存曲線の作成
import matplotlib.pyplot as plt
result = cph.predict_survival_function(df_workers.iloc[:, 1:7])
sample1 = result.iloc[:, 1]
plt.plot(sample1.index, sample1)
plt.show()以下のようなグラフが出力されます.
補足 要因(変量)が1つの場合
生存時間データの要因が1つの場合は,ログランク検定または一般化ウィルコクソン検定を行います.群間の比較を行います.










