p値とは
p値(p-value)とは統計学における仮説検定で,設定した仮説が正しいかを判定するための基準となる値になります.
統計学的なp値の定義は以下になります.
『帰無仮説が正しいと仮定したときに,観測された値以上に極端な値が出る確率』
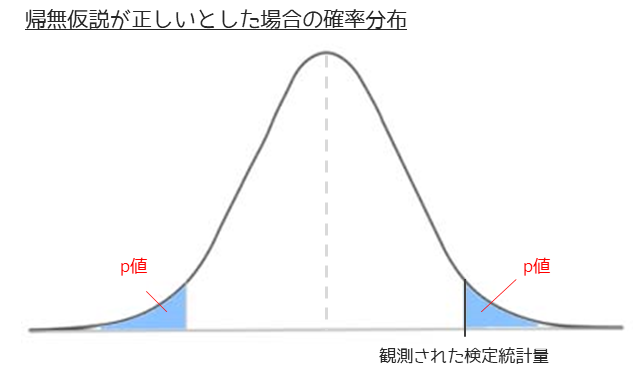
検定結果として計算されたp値は,観測された値(標本から得られた検定統計量)以上に稀な値が出る確率を示します.p値は確率なので0から1の値の値を取ります.
仮説検定において標本から得られたp値が十分に小さい場合,「帰無仮説は正しい」という仮定は間違っている可能性が高いと判断し対立仮説を採択します.
一般的にはp値<有意水準α=0.05の場合に帰無仮説を棄却して,対立仮説を採択します.
統計学では一般的に有意水準α=0.05として設定し,p値が0.05未満の際に帰無仮説を棄却します.これによりデータ分析をする際の検定結果として,p値が0.05を超えたか超えないかが重要視されがちです.
では,一般的に使われる有意水準α=0.05はどのように決められたのでしょうか?結論としては約100年前からの慣習になります.統計学者として有名なフィッシャーが,自身で恣意的と認めながら指標として用いたのが起源になります.つまり,有意水準α=0.05という値には科学的な根拠はありません.
有意水準α=0.05という値は実際にはそれほど重要な値ではないので,検定結果を記述する際は有意差の有無だけでなく,p値を記載するようにしましょう.
仮説検定についての考え方や,手順については以下のページで解説しています.
2016年にp値の解釈について,アメリカ統計学会が声明を発表しており多くの論文で引用されています.より深く理解したい方は読んでみてください.
The ASA Statement on p-Values: Context, Process, and Purpose (2016) by Wasserstein & Lazar
p値と検定統計量の関係(初学者の方向け)
仮説検定について学び始めたばかりの方は,検定統計量やp値,限界値といった統計用語を混同しがちです.
仮説検定の用語は以下のように,確率分布を用いて理解するとわかりやすいです.
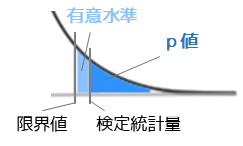
帰無仮説の下での確率分布の右側(上端)を示した図です.確率分布の面積は確率を表し,p値は既に説明したように観測された値より極端な部分(外側)の面積になります.
観測された値つまり,標本から得られた統計量を検定統計量と言います.
限界値より稀な値を取る確率(面積)を有意水準αと言います.
仮説検定によってはp値を求めることができない手法があります.p値を求めることができない検定手法では,検定統計量を計算して限界値と比較することで有意差判定を行います.
有意水準→限界値,検定統計量→p値の変換は帰無仮説が,どのような確率分布に従うかによって計算方法が異なります.特に有意水準→限界値を求める際は,t分布表のような専用の検定表を用いる必要があります.
p値とサンプルサイズの関係
p値で誤解されやすいのが,「p値は比較した2群の母集団の差を意味する」という考え方です.しかし,p値は2群の母集団の差を示す統計量ではありません.
以下の図は,2群の平均値の差の検定を表した図になります.
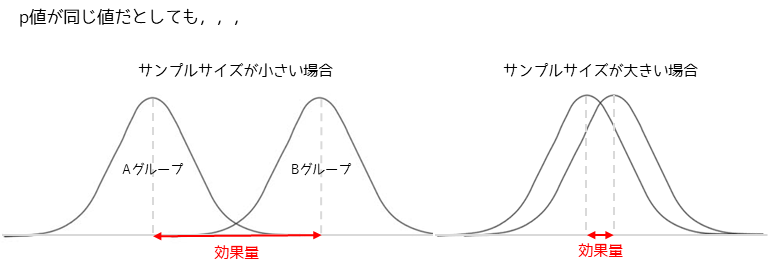
p値が同じ値であった場合,サンプルサイズが大きい方が母集団の差が小さいという性質があります.言い換えると,サンプルサイズが大きい場合は僅かな差であっても有意差判定されるため,p値があまり意味を持たなくなります.
例えばn=10,000のような非常にサンプルサイズのデータに対して仮説検定を行う場合は,検定結果をp値だけで判断するのでなく効果量を用いて判断することが重要です.
効果量とはサンプルサイズに依存しない統計量で,母集団の差を示します.
p-hacking
p-hackingとはp値を都合の良いように操作することを言います.つまり,有意水準を下回るのようなp値を計算することです.
p-hackingを意図的に行うことは問題ですが,仮説検定を行う際に無意識に行ってしまう場合があります.よく行ってしまうp-hackingの例は以下になります.
【p-hackingの例】
① n=40で検定を行ったらp=0.06だったのが,n=60で検定を行ったらp値<0.05となったので有意差判定を行った
② 複数のデータの組み合わせで仮説検定を行い,有意差があった組み合わせのみを仮説検定の結果とした
①についてはサンプルサイズとp値の関係で説明したように,p値はサンプルサイズが大きくなるほど小さい値が出やすくなります.サンプルサイズを大きくして仮説検定を繰り返し行った場合,本当は差がないのに統計的に有意差ありとしてしまう確率が上がってしまいます(第一種の過誤).
②は統計学における多重性の問題になります.多くの実験を繰り返すことで,たまたまp値が有意水準を下回る可能性が上昇します.複数回検定を行った上での有意差と,1回のみ行った有意差では全く違う意味を持つので検定結果は全て報告する必要があります.
複数のデータに対して仮説検定を行う場合は,予備実験を行いその結果から効果がありそう(有意差がありそう)なデータを絞り,再度仮説を設定した上で本実験を行うという方法があります.特定のデータのみを報告する結果の対象にしたい場合に,再度データを取り直すというのがポイントです.
再度実験を行うことができない場合は,多群に対する検定方法として有効な分散分析や多重比較を行う必要があります.









