フリードマン検定とは
フリードマン検定とは,対応のある3群以上の差の検定(対応のある一次元配置分散分析)のノンパラメトリック版です.順序尺度以上のデータに対して用いることができます.
ウィルコクソンの符号順位検定を,3群以上対して使えるようにした検定方法になります.検定統計量はΧ2分布に近似的に従います.
以下の図はフリードマン検定の考え方になります.
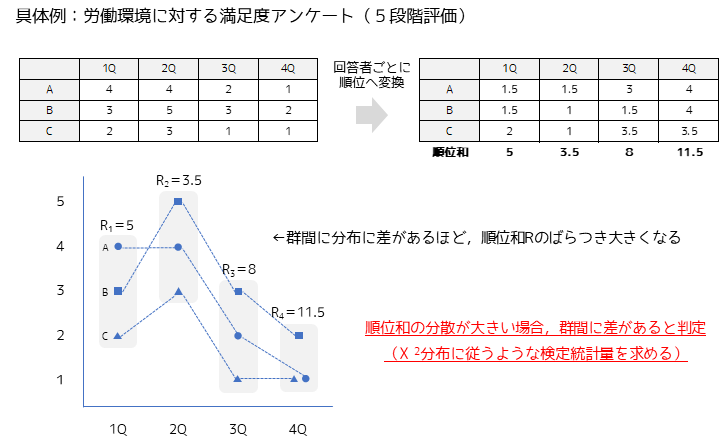
3群以上のデータをサンプル(回答者)ごとに順位データに変換して,各群の順位の合計値(順位和)を計算します.群間に差があるほど順位和のばらつきは大きくなるため,順位和の分散が大きい場合群間に差があると判定します.
フリードマン検定の手順
フリードマン検定は以下の手順で行います.
① 仮説の設定
帰無仮説は「3群以上の母集団に差がない」,対立仮説は「3群以上の母集団に差がある」として設定します.
② 有意水準の決定
p値を求める際にカイ二乗検定を行なうため有意水準α=0.05とします.片側検定(右側)のみで両側検定はありません.
③ 検定統計量の算出
具体的な計算手順は,Excelを用いた方法で解説しています.
④ p値の算出
検定統計量からp値を算出します.小標本の場合は求めません.
⑤ 有意差判定
○大標本の場合
p値<0.05であれば,帰無仮説は棄却されて対立仮説を採択 → 「3群以上の母集団に差がある」
p値\(\geq\)0.05であれば,帰無仮説は棄却されない → 「3群以上の母集団に差があるとは言えない」
○小標本の場合(サンプルサイズが3群で9以下,4群で5以下)
検定統計量>限界値であれば,帰無仮説は棄却されて対立仮説を採択
検定統計量\(\leq\)限界値であれば,帰無仮説は棄却されない
仮説検定の考え方や用語については,以下のページで解説しています.
検定結果を間違えたくない方へ
Excelを用いた計算方法より簡単・正確に,フリードマン検定の検定結果を調べることができる統計解析アプリStaatAppを販売しております.
StaatAppではフリードマン検定以外にも様々なノンパラメトリック検定をクリック操作だけで実行することができます.詳細は以下のページをお読みください.
》StaatAppで行う仮説検定
》統計解析アプリStaatApp
例題で用いるデータと仮説の設定
例題では以下のサンプルデータを用います.ある会社の社会人10人に対して四半期ごとに労働環境に関する満足度調査をした結果になります.(5段階評価で5が最も満足度が高いとします.)

帰無仮説は「四半期ごとの労働環境の満足度に差がない」となり,対立仮説は「四半期ごとの労働環境の満足度に差がある」と設定します.
有意水準α=0.05で検定は行います.
Excelを用いた計算手順
Excelを用いた検定統計量とp値の計算手順について説明します.
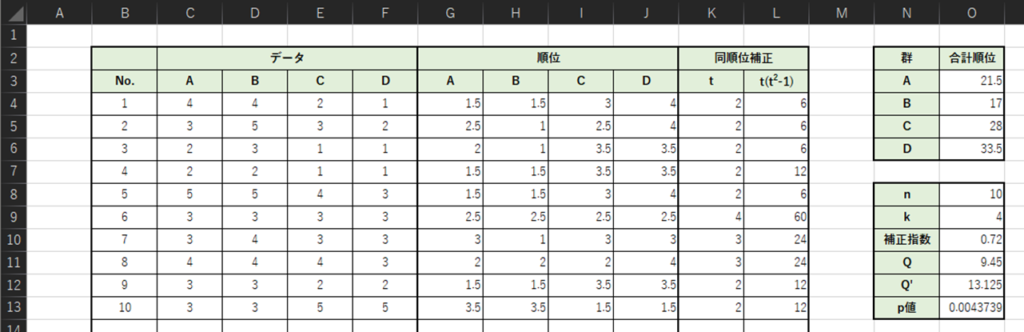
以下のような表を作成して,検定統計量Qとp値を求めます.(例題データの変数名を1Q→A,2Q→B,…,として入力しています.)
各セルの入力式は以下になります.
・G4:=RANK.AVG(C4,$C4:$F4,0)
・L4:=K4*(K4^2-1)
・O3:=SUM(G4:G13)
・O8:=COUNT(B:B)
・O10:=1-(SUM(L:L)/(O9*(O9^2-1)*O8))
・O11:=(12/(O8*O9*(O9+1)))*(O3^2+O4^2+O5^2+O6^2)-3*O8*(O9+1)
・O12:=O11/O10
・O13:=CHISQ.DIST.RT(O12,O9-1)
入力式と計算手順について解説します.
① データを入力する【B-F列】
サンプル番号と値(評価値)を各1列にデータを入力します.
② 順位を求める【G-J列】
入力した値を順位データに変換します.順位は同じ個体(行)ごとに求めます.
順位データはRANK.AVG関数を用いて計算します.RANK.AVG関数の引数は以下になります.
RANK.AVG(“順位に変換する値”,”順位の対象となるデータ群(行)”,0)
※ 例題では値が大きいほど順位が高くなるように計算します.
③ 補正指数を求める(タイデータがある場合)【K列】【L列【O10】
順位データに同じ値(タイデータ)がある場合,検定統計量を補正するために必要な補正指数を求めます.補正指数は以下の式で求めることができます.
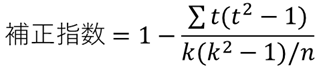
tはタイデータの個数,kは群数,nはサンプルサイズになります.
補正指数を「O10」セルで計算するために,「K列」・「L列」で必要な値を計算します.
回答者1では順位データが1.5が2つあるためt=2となります.回答者4は同順位のデータが2つずつあるので「L4」セルはt(t2-1)の値を2倍にします.
④ 各群の合計順位を求める【O3-6】
検定統計量の計算に必要な各群の合計値(順位和)を計算します.
行ごとに合計値を計算するためにSUM関数を用います.
⑤ 検定統計量Qを求める【O11】
検定統計量Qを計算します.検定統計量Qは以下の式で計算します.

Riは各群の順位和,nはサンプルサイズ(回答者数),kは群数(調査回数)になります.
⑥ 補正後検定統計量Q‘を求める(タイデータがある場合)【O12】
タイデータがある場合は,補正指数を用いて検定統計量を補正します.補正式は以下になります.
Q’ = Q / 補正指数
⑦ p値を求める【O13】
検定統計量または補正後検定統計量からp値を求めます.検定統計量はΧ2分布に従うのでCHISQ.DIST.RT関数を用いて計算します.CHISQ.DIST.RT関数は検定統計量からΧ2分布の右側確率を求めることができます.
引数は以下になります.
CHISQ.DIST.RT(“検定統計量”,”自由度”)
自由度は”群数-1”で求めることができます.例題では自由度は3です.
例題ではp値が0.00437…となり有意水準未満となったので,帰無仮説は棄却され「四半期ごとに労働環境に対する満足度に差がある」といった結論を得ることができます.
Excelを用いた計算手順(小標本の場合)
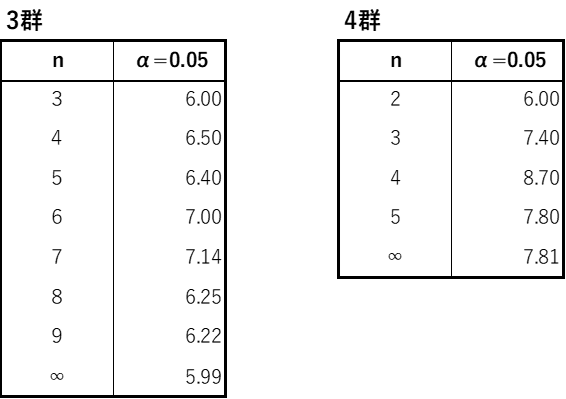
サンプルサイズが小標本の場合に,Χ2分布を用いてp値を計算すると若干厳しい結果となるため専用の検定表を用います.検定表は補足①にあります.
小標本とは3群で9以下,4群で5以下の場合になります.
例題において回答者が3人であった場合,4群の検定表からn=3の行を見て限界値は7.40であることがわかります.
Pythonを用いた計算方法
Pythonを用いたp値の計算方法について,サンプルコードは以下になります.
from scipy import stats
A = [4, 3, 2, 2, 5, 3, 3, 4, 3, 3]
B = [4, 5, 3, 2, 5, 3, 4, 4, 3, 3]
C = [2, 3, 1, 1, 4, 3, 3, 4, 2, 5]
D = [1, 2, 1, 1, 3, 3, 3, 3, 2, 5]
result = stats.friedmanchisquare(A, B, C, D)
print(result)
==> 実行結果
FriedmanchisquareResult(statistic=13.124999999999984, pvalue=0.004373937634328744)PythonではScipyライブラリを用いて,フリードマン検定のp値を計算することができます.
出力結果はpvalue=0.0043739..となっており,Excelでの計算結果と一致することがわかります.
補足① フリードマン検定表
補足② データの前提条件
フリードマン検定を行う際の扱うデータの前提条件について紹介します.
① 対応のある場合
フリードマン検定は対応のないグループ(別個体)のデータに対しては用いることができません.対応のない場合は,クラスカル・ウォリス検定を行う必要があります.
② 母集団が正規分布に仮定できない場合
フリードマン検定はノンパラメトリック検定の1つです.扱うデータの母集団が正規分布に従い,等分散性がある場合は対応のある一元配置分散分析を行います.
③ データが3値以上の場合
扱うデータが順位データのように3値以上である必要があります.2値データ(Yes/No)の場合はマクネマー検定を行います.
補足③ 多重比較との関係性
フリードマン検定では,3つ以上グループがある場合にどのグループとどのグループが異なるかまでは判断することができません.これらのことを判断したい場合は,「多重比較」という分析を行います.










