統計学の2つの種類や統計学でできることについて紹介します.
統計学とは

統計学とはそのままのデータでは分かりづらいデータの特徴や関係性を,統計量や図表を用いることで調べる・活用する学問です.
言い換えると正しく・上手くデータを扱うための学問になります.
統計学の種類
統計学は記述統計学と推測統計学の2つがあります.記述統計学と推測統計学では調べたい対象が異なります.
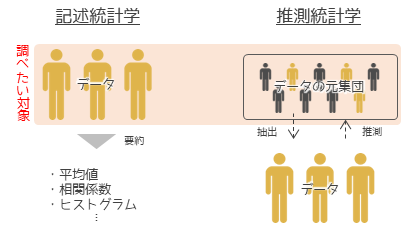
記述統計学では調べたい対象が分析を行う,データそのものになります.扱うデータ自体の特徴や分布,関係性を調べます.具体的には平均値や中央値などの基本統計量や相関係数,分布を表現するヒストグラムが記述統計学に分類されます.
記述統計学は統計学の中でも最も古典的な分野で,普段の生活から比較的馴染みがある分野になります(平均値や散布図など).
推測統計学では調べたい対象がデータ自体ではなく,データを抽出する元となった集団(母集団)になります.調べたい対象を全て調べることが現実的に難しい・コストがかかるという理由から,調べたい対象を代表する個体(標本)を抽出して,そのデータの振る舞いから特性を推測するのが推測統計学です.つまり,推測統計学では限られたデータから普遍的な事実を推測することができます.
統計学が最も威力を発揮するのが推測統計学で,本サイトでも推測統計学を重点的に解説してます.具体的には区間推定や仮説検定,多変量解析といった方法があります.
統計学でできること
統計学を用いたデータ分析では以下の3つのことができます.
① データの特徴を把握する
記述統計学で説明した統計量を用いることで,データの性質や分布を調べることができます.データの特徴を把握することで,そのデータの意味を理解することや新しい発見をすることができます.
② データ間の関連性を調べる
複数の種類のデータ(変数)間での関連性を調べることができます.関連性を示す代表的な手法が相関になります.相関を算出することで,2変数の直線関係を調べることができます.
仮説検定では複数の標本を比較することで,母集団に差があるか・調べたい事象による効果があったのかを調べることができます.
③ データを予測する
データの特徴や関連性から予測式を作成して,未知のデータを予測することができます.回帰分析では既存データから回帰直線(予測式)を作成して,変数を代入することによって予測したい値を求めることができます.
より具体的な目的ごとの解析手法は,以下のページで解説しています.
統計学は科学の共通言語
統計学はどのような分野においても,数値情報を用いる限り必ず使用される学問です.様々なデータや分析結果を統計学の規則に従って,説明・記述することで科学的なコミュニケーションを取ることができます.
統計学において共通認識は重要で,共通認識は既往研究や過去の慣習から生まれます.例えば,仮説検定における有意水準α=0.05は科学的な根拠がある訳ではなく,慣習としてよく用いられます.
統計解析の手法は多種多様ですが,まずはよく用いられる手法を使用することをおすすめします.マイナーな手法を用いて結果を示しても,読む人がそれを理解できない場合意味のない結果となり得るからです.Staatで紹介している手法のほとんどが一般的に使われる解析手法なので,本サイトから適切な方法を探してみるのも良いかもしれません.










