仮説検定とは
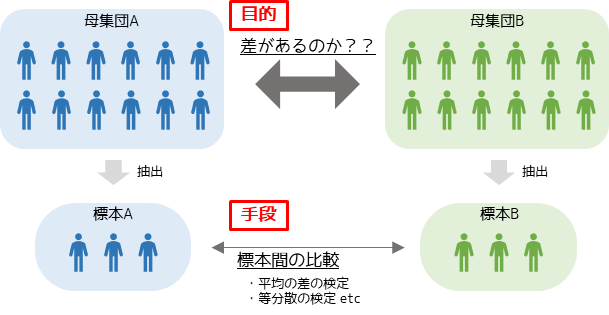
仮説検定とは,標本を用いて母集団に統計学的に差があるかを判断する方法です.言い換えると,あるデータが得られた際にそのデータの差は偶然(誤差の範囲)と考えてよいのか,違うデータである可能性が高いと考えるかを判定する統計的な手法になります.
比較する際に用いる統計量の種類や標本数によって様々な検定方法があります.
仮説検定のフロー
仮説検定には決まった手順が存在します.どのような検定方法を行なう場合でも,以下のような基本的な手順は同じです.
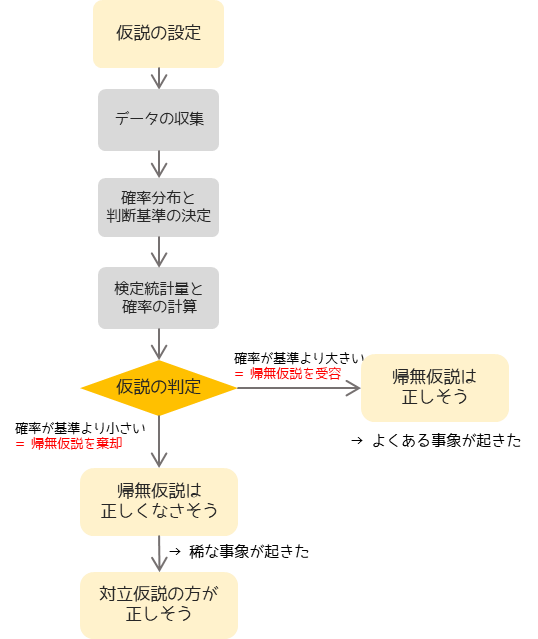
仮説の設定では,棄却したい帰無仮説と採択したい対立仮説を設定します.
確率分布と判断基準の決定では,検証するデータ(母集団)がどのような確率分布に従うのか,どの程度の確率で帰無仮説を棄却するのかという判断基準(有意水準)を決めます.
帰無仮説の下での検定統計量を計算し,確率分布から検定統計量以上に極端な値になる確率(p値)を計算します.
仮説の判定では,判断基準より求めた確率が小さい場合は帰無仮説を棄却,求めた確率が大きい場合は帰無仮説を採択します.
帰無仮説が棄却された場合,帰無仮説は正しくないつまり対立仮説の方が正しそうといった結論を得ることができます.(背理法)
帰無仮説が棄却されなかった場合,帰無仮説が正しくないと言うことができず,対立仮説が正しそうといった結論を得ることができません.
仮説検定のよくある誤認識が,「仮説検定はp値を算出すること」です.ここまで解説したように,仮説検定は”仮説の設定”から”仮説の判定”までの一連の手順を意味します.
正しく確率的に判断するためにはデータを収集する前段階から仮説を設定していることが重要で,得られたデータからなし崩し的にp値を算出する手順は正しい仮説検定とは言えません.
帰無仮説と対立仮説
検定では母集団に関する仮説が正しいか判断するために,帰無仮説と対立仮説を設定します.

帰無仮説とは検定で棄却したい,つまり否定したい内容になります.検定は差があることを判定するのが目的であるので帰無仮説は「特定の値と差がない」,「群間に差がない」といった内容が帰無仮説として設定されます.
対立仮説は検定の結果,帰無仮説が棄却された際に代わりに採択される仮説です.対立仮説は「特定の値と差がある」「群間に差がある」といった内容が設定されます.
重要なのは検定結果として主張したい内容は,対立仮説に設定することです.
群間に差がないことを判断するために検定を行い,帰無仮説が棄却されなかった場合でも群間に差がないと積極的に言うことはできません.(差がないことは確率的によく起きることのため)
仮説の判定方法
ここからは判断基準の決定方法や検定で用いる用語を説明するために,最も基本的な検定方法である”母平均の検定”を例として用います.
母平均の検定は,特定の値と観測された標本平均を比較して,それらに差があるかを判定します.
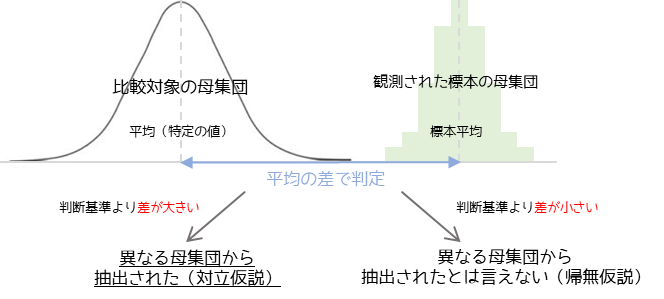
判定する際には特定の値と標本平均の差が判断基準である境界値より大きいかどうかという考え方をします.
境界値を統計学では限界値(臨界値)と言い,事前に決めた有意水準から求めることができます.
有意水準とは
有意水準とはどの程度の精度で帰無仮説を棄却するかの判断基準です.
例えば有意水準α=0.05(αは確率を表します)とすると,比較対象の母集団の全体面積から5%以下にあたる端の値は稀な事象として扱う(=異なる母集団である確率が高い)ということを意味します.
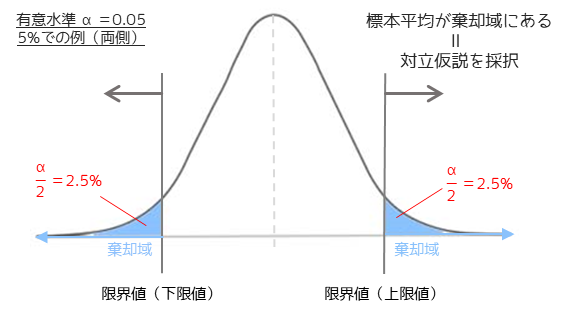
両側検定において有意水準α=0.05の場合,両側で合せて5%なので片側はそれぞれ2.5%となります.
有意水準は特段理由がない限りは,両側で5%として検定を行います.
有意水準から限界値は分布表を用いることで求めることができます.母平均の検定の1つであるt検定を行う場合,以下のようなt分布表(両側)を用いることで限界値を求めることができます.
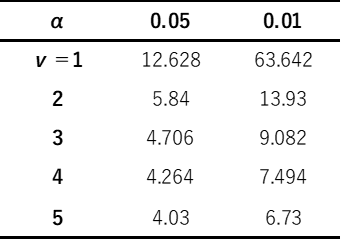
有意水準α=0.05で自由度v=4の場合,限界値(下限値)は-4.264で限界値(上限値)は4.264と求めることができます.
※ 自由度はサンプルサイズから決まります.
検定統計量とp値
母平均の検定では標本平均と限界値を比較することで,仮説の判定を行うことができます.
2群を比較したい場合などは,どちらの母平均も不明なため差の大きさを限界値と標本平均の差で判断することができません.そこで,仮説の判定を行うために求める値が検定統計量です.
検定統計量が限界値より大きいかどうかで仮説の判定を行います.検定統計量は行う検定方法によって求め方が決まっています.
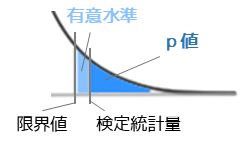
検定統計量よりも外側の値が観測される確率(確立分布での面積)をp値と言います.限界値より外側の観測される確率が有意水準であるため,有意水準とp値を比較することで仮説の判定を行うことができます.
Excelや統計ソフトでは,検定統計量を求めずにp値を直接求めることができます.いきなりp値を求めることで,限界値や検定統計量を求める手間を省くことができます.
両側検定と片側検定
検定の種類によっては両側検定に加えて片側検定という方法があります.
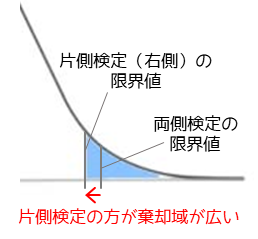
片側検定とは片方(左側または右側)の確率だけで有意水準αとする検定方法です.片方だけで有意水準αとするので同じ有意水準での両側検定の棄却域と比較して,棄却域は広がります.
つまり,片側検定の方が両側検定より帰無仮説を棄却しやすくなります.
片側検定は以下のような場合に用いることがあります.
・標本平均が明らかに特定の値より大きくなる(もしくは小さくなる)ことが分かっている場合.2群の比較であれば,標本間の大小関係が明らかなとき.
・標本平均が特定の値より大きいこと(もしくは小さいこと)のみを調べたい場合.
上記のような理由以外(帰無仮説を棄却したいからなど)で,片側検定を行うのは統計学的によくありません.
仮説検定の種類
統計的仮説検定には様々な種類があります.扱うデータの種類や標本数によって用いる検定方法が異なります.
一般的に使われている統計手法を標本数と比較に用いる統計量の観点から,下記のページで整理しています.どの仮説検定を行えばよいか迷っている方は読んでみてください.
仮説検定をより正しく理解したい方へ
本ページでは仮説検定について,最低限知って欲しい事項について解説をしました.
より正しく仮説検定を行い,結果の解釈を行うためには以下のページの内容も理解してください.
》p値が有意水準を下回れば良しではない!(p値とは)
》仮説検定における2つの誤り(第一種の過誤・第二種の過誤とは)
》仮説検定の結果はp値だけでは不十分?(効果量とは)










