二元配置分散分析とは
二元配置分散分析とは,要因が2つ以上の場合の分散分析になります.二元配置分散分析では各要因の効果に加えて,変数間の交互作用についても評価することができます.
一元配置分散分析との違いや交互作用については,以下のページで解説しています.
二元配置分散分析の考え方は以下の図になります.業界ごと・副業の有無ごとに年収を比較した例になります.
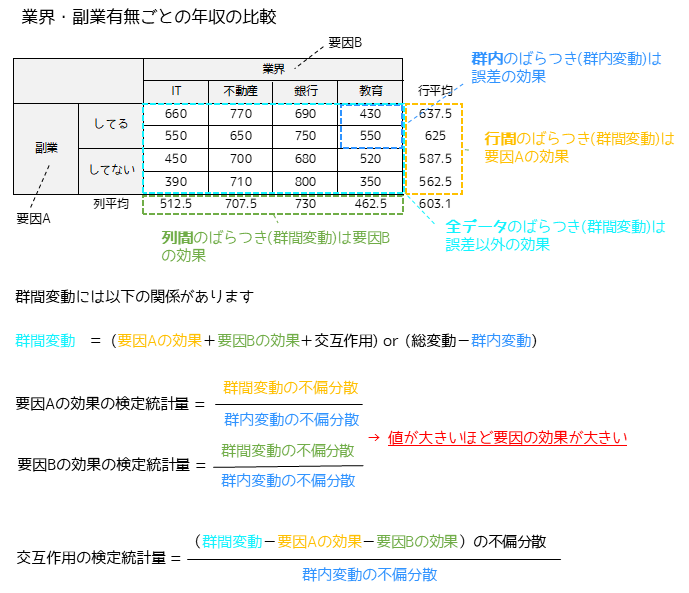
二次元配置分散分析では「副業有無によって年収に差があるか」「業界の違いによって年収に差があるか」「副業の有無と業界の違いに交互作用があるか」の3点について判定することができます.
比較するセル内(業界内)のデータのばらつきを誤差の効果,行間(副業有無)のデータのばらつきを要因A(副業有無による)の効果,列間(業界ごと)のデータのばらつきを要因B(業界の違いによる)の効果と考えます.
交互作用は群間変動から要因Aの効果と要因Bの効果を除いた変動になります.誤差の効果に対して各要因の効果,交互作用が大きい場合に値が大きくなるような検定統計量を求めます.
検定統計量は分散の比になるため有意差判定にはF分布を用います.
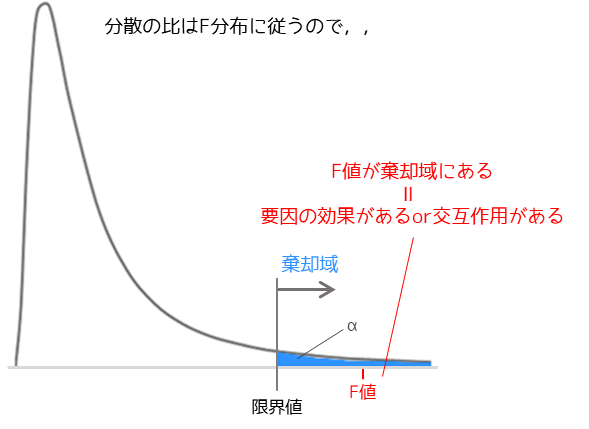
要因Aの検定統計量が棄却域にある場合,要因Aによる効果があるとなります.例では「副業をしている人としていない人で年収に差がある」といった結論を得ることができます.
二元配置分散分析の手順
二元配置分散分析は以下の手順で行います.
① 仮説の設定
帰無仮説は以下の3つになります.
・「要因Aの母平均に差がない」
・「要因Bの母平均に差がない」
・「要因Aと要因Bに交互作用がない」
対立仮説は以下の3つになります.
・「要因Aの母平均に差がある」
・「要因Bの母平均に差がある」
・「要因Aと要因Bに交互作用がある」
② 有意水準の決定
有意水準α=0.05または0.01とします.一般的には0.05で設定されます.
③ 検定統計量の算出
群内変動と群間変動から検定統計量を求めます.
④ p値の算出
検定統計量とF分布表からp値を求めます.Excelの場合,検定統計量と同時にp値を算出できます.
⑤ 有意差判定
・有意水準<p値の場合,帰無仮説は棄却されない →「群間に差があるとは言えない」または「交互作用があるとは言えない」
・有意水準\(\geq\)p値の場合,帰無仮説は棄却され,対立仮説が採択される → 「群間に差がある」「交互作用がある」
仮説検定の考え方や用語については,以下のページで解説しています.
分散分析を行なうならStaatApp!
統計アプリStaatAppを使用すれば,Excelを用いるより簡単に二元配置配置分散の結果を得ることができます.
StaatAppでは二元配置分散分析以外にも多元配置分散や様々な仮説検定をマウス操作だけで実行することができます.無料機能で分散分析は実行可能なので,ご自由にダウンロードしてお使いください.
》StaatAppで行う分散分析
》統計解析アプリStaatApp
例題で用いるデータと仮説の設定
例題では以下のサンプルデータを用います.4つの業界で働いている社会人ごとに年収と副業の有無を調査した結果になります.

帰無仮説は以下の3つになります.
・「副業の有無で年収の差はない」
・「業界ごとに年収の差はない」
・「副業の有無と業界に交互作用はない」
対立仮説は
・「副業の有無で年収に差がある」
・「比較した業界で年収に差がある」
・「副業の有無と業界に交互作用がある」
と設定します.
有意水準α=0.05で検定は行います.
Excelを用いた検定手順
Excel画面を用いて説明をします.使っているExcelのバージョンはOffice2016になります.
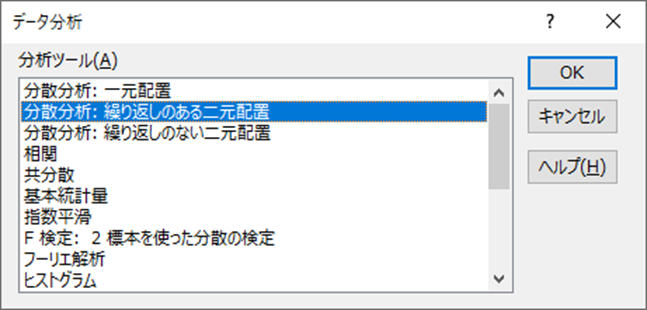
二元配置分散分析を行うツールを選択するために,「データ」タブの「データ分析」をクリックします.

出てきた「データ分析」ウィンドウから,「分散分析: 繰り返しのある二元配置」をクリックして「OK」を選択します.
※ 二元配置分散分析における”繰り返しのある”とは,IT業界かつ副業をしてる回答者が複数いる例題のように,セル内のデータ数が2以上の場合です.
「分散分析: 繰り返しのある二元配置」における入力例は以下のようになります.
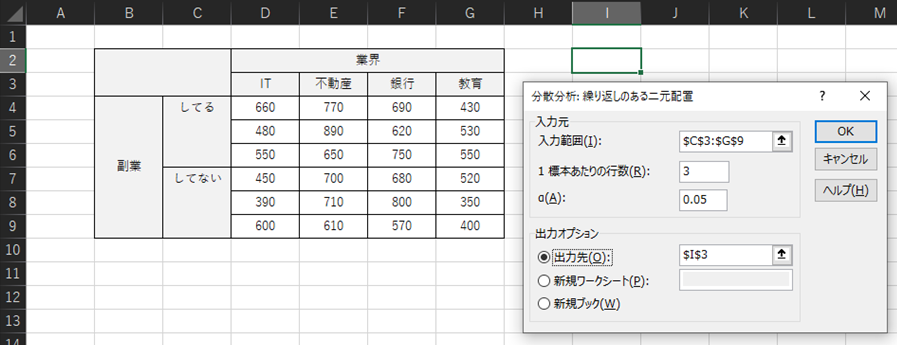
「入力範囲(I)」では事前に入力したデータのセルを選択します.データの範囲はラベルが入力されている行と列(3行目とC列)まで含めます.
「1標本あたりの行数(R)」は1つのセルのデータ数を入力します.例題では3になります.
「α(A)」では,二次元配置分散分析の有意水準を入力します.一般的に使用する有意水準α=0.05とする場合は,”0.05”を入力します.
「出力先オプション」では「出力先(O)」を選択して任意のセルを選択してください.同じシート内の空白のセルを選択すると出力結果が見やすいです.
以上の項目を入力して「OK」をクリックすると,出力指定したセルに二元配置分散分析のp値と検定統計量が出力されます.
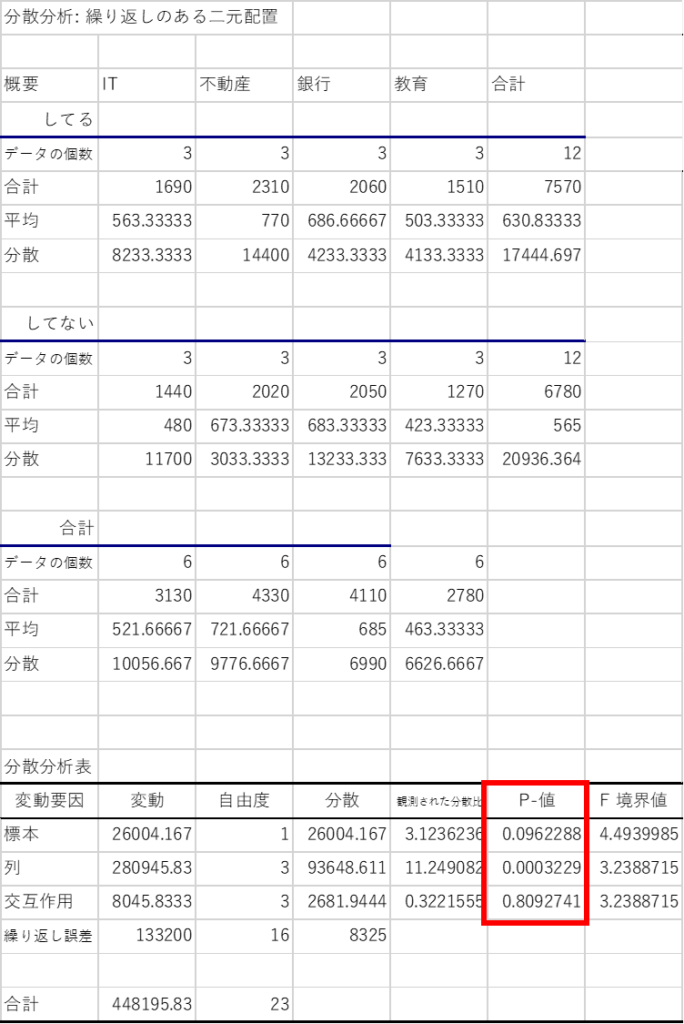
分散分析表の変動要因のうち「標本」は行項目,「列」は列項目を示しています.
例題では,標本のp値が0.096..であるので帰無仮説は棄却されません.列のp値は0.00032..で p値 < 有意水準α=0.05であるため帰無仮説は棄却され対立仮説が採択されます.よって「業界によって年収は異なる」といった結論が得られます.
交互作用のp値は0.809であるため帰無仮説は棄却されず,「副業の有無と業界に交互作用がない」といった結論が得られます.
補足① 片側検定について
分散分析では,片側検定はなく両側検定のみになります.
補足② 交互作用と多重比較の関係について
二元配置分散分析では,3群以上の標本に対して母平均に差があるかを調べます.検定結果としてはどれかの標本に差があるという判断をすることができますが,要因ごとのどの群とどの群に差があるかを特定することはできません.
3群以上の標本に対して2つの群ごとに検定を行い,どの群とどの群が異なるかを調べる際は多重比較という手法を用います.
二元配置分散分析の結果として,交互作用がある場合は要因Aと要因Bは切り離して考えることはできないため要因Aの群と要因Bの群(全てのセル)に対して多重比較を行います.
交互作用がない場合は有意差があった要因ごとに群間の比較を行います.
補足③ 一元配置分散分析を行う前提条件
二元配置分散分析を行う際の扱うデータの前提条件について紹介します.
① 対応のない場合
二元配置分散分析は対応のある群(同一個体)のデータに対しては用いることができません.対応のある場合は,混合効果二元配置分散分析を行う必要があります.
② 正規分布に従う
分散分析は,パラメトリックな検定になります.用いるデータが正規分布に従うと仮定できる場合に使うことができます.正規分布でない場合は,ノンパラメトリック検定であるクラスカル・ウォリスの検定を行います.
③ 比較するグループの分散が等しい
比較する群の分散が等しい場合に二元配置分散分析を行います.3群以上の分散はバートレット検定で調べることができます.分散が等しくないときは,ウェルチの検定を行います.










