【例題解説】対応のあるt検定の計算手順

対応のあるｔ検定について解説をします．

具体的な計算手順と，検定を行う際に注意すべき点を補足事項として整理したので最後まで読んで正しい検定方法を確認してみてください．

対応のあるｔ検定とは

対応のある検定とは，２つのグループの比較において同じ個体から取得したデータが異なるか判断するために行う統計的手法です．

特に，対応のあるｔ検定とは２つのグループの母平均を比較することで２つのグループに差があるのかを判断します．対応のあるｔ検定を母平均の差の検定とも統計学では言います．

よく使われる例として，ある30人の被験者に対して投薬を行いその薬に効果があったか（＝被験者の体調を示すデータに差があるか）を調べる際に用いられます．

対応のあるｔ検定の計算手順

具体的な計算手順を，例題を使って説明します．

一人暮らしをしている40人の大学生に，実家で生活していた時と現在の一日の平均スマホ使用時間を調査しました．この際に，「一人暮らしはスマホの使用時間に影響があるか」という仮説を対応のあるｔ検定を用いて分析します．

調査した結果は以下の表のようになりました．

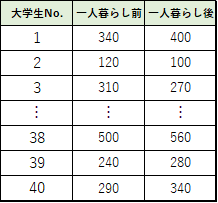
ｔ検定を行うために，まず２つのグループの被験者ごとの差を求めます．

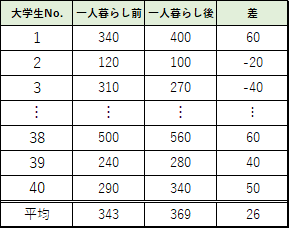
今回の例では，母分散が分からないので不偏分散を用いたｔ検定を行います．そこで，先程のデータから不偏分散を求めます．

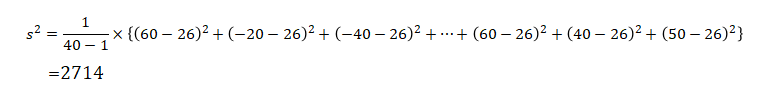
求めた不偏分散を用いて，検定統計量を求めます．検定統計量は以下の式で求めることができます．

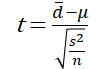
ここで，\(\bar{d}\)は平均の差，\(\mu\)は差の母平均，\(n\)はサンプルサイズになります．また，差の母平均は母平均が等しいことを検定しているため対応のあるｔ検定では常に\(\mu\)＝０となります．

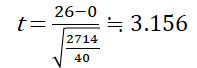
求めた検定統計量とｔ分布表からｐ値を算出します．今回の検定では有意水準は5%（α＝0.05）で自由度は39（＝サンプル数－１）とします．また，差があるかどうかを調べるためｔ分布表は両側を使います．

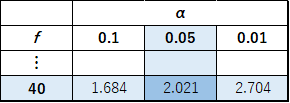
両側のｔ分布表から，自由度40のときｔ検定統計量が2.021でｐ値＝0.05なので，自由度39でｔ検定統計量が3.156の場合，p値＜0.05であることが分かります（正確には自由度39のｐ値を求める必要がありますが，上記の結果からｐ値が棄却域にあることが明らかです）．このことから，ｔ検定統計量は自由度39のｔ分布の棄却域に入っており「有意水準5%において、帰無仮説を棄却し、対立仮説を採択する」といった結果になります．

帰無仮説は対応のあるｔ検定において”差がないこと”になるので今回の帰無仮説は「一人暮らしはスマホの使用時間に影響はない」となります．そして対立仮説は”差があること”つまり「一人暮らしはスマホの使用時間に影響がある」となり対立仮説が採択されたことから，一人暮らしはスマホの使用時間に影響があるといった結論となります．

ここまでが，対応のあるｔ検定の実践的な具体手順でした．計算手順のみを解説するため，敢えて説明しなかったことも多いためここから補足をしていきます．

まずは，対応のあるｔ検定の計算手順を整理します．

例題では，最後に帰無仮説・対立仮説の確認をしましたが本来の流れは最初に帰無仮説と対立仮説を立てて有意水準を決めます．そして，検定統計量を求めたあとに帰無仮説に対応した検定（片側か両側）を選択して検定を行い結論を導きます．

補足① 帰無仮説と対立仮説の立て方

対応のあるｔ検定は，２つのグループの母平均の差を比較するための手法でした．

帰無仮説は「２つのグループの母平均に差がないこと」とします．そして，対立仮説では「２つのグループの母平均に差があること」とします．

補足② 両側検定と片側検定の選び方

対応のあるｔ検定は，検定統計量を求めたあとにｔ分布を用いて両側検定もしくは片側検定を行います．

計算手順で示した例題では，スマホの使用時間が「一人暮らしによる影響があるか」＝「一人暮らしの前後で差があるか」ということを判断することが目的でした．この場合は，２つのグループは異なるかどうかを判断するだけなので両側検定を行います．

２つのグループのうちどちらかが明らかに大きいまたは小さいといった判断をしたい場合は片側検定を行います．

厳密な基準があるわけではないので，検定の目的によって使い分けてください．

補足③ 片側検定の手順

例題のサンプルに対して，「一人暮らしをしたらスマホの使用時間が長くなる」ことを判断したいとします．この際の帰無仮説は「一人暮らしはスマホの使用時間に影響はない」となり，対立仮説は「 一人暮らしをしたらスマホの使用時間が長くなる 」となります．このような大小を判断する対立仮説を場合は，片側検定を行います．

検定統計量は，両側検定で求めたものと同じ3.156を採用します．そして，以下のような片側のｔ分布表を用います．

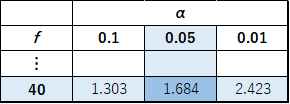
この表より，自由度40では検定統計量が1.684でｐ値が0.05であることがわかります．これよりｐ値>0.05とうことが分かります．よって，帰無仮説が棄却され対立仮説が採用されます．

対応のあるｔ検定の片側検定により，例題において「一人暮らしをしたらスマホの使用時間が長くなる」という結論が得られました．これが，片側検定の手順になります．

両側検定と片側検定の違いは，使用するｔ分布表の違いになります．それぞれの検定にあったｔ分布表を用いるようにしましょう．

また，片側検定では右側と左側の２つの検定があります．使い分け方としては，２グループの標本平均の差が正か負のどちらを明らかにしたいかで判断します．言い換えると，検定統計量を求める際に”標本平均の差＝郡B – 郡A”で求めるとします．このとき，”群A＞群B”を明らかにしたい場合は左側の片側検定を行います．逆に”郡A＜郡B”を明らかにしたい場合は右側の片側検定を行います．

今回の例題では，”郡A＜郡B”つまり標本平均の差が正であることを明らかにしたいため右側の片側検定を行いました．

補足④ 対応のあるｔ検定の前提条件

最後に，ここまでに紹介した対応のあるｔ検定を行う際に用いるデータについて説明します．

① 正規分布に従うこと
　ｔ検定はパラメトリックな検定つまり，データが正規分布に従うことを前提条件に行います．正規分布に従わない場合や分布が不明なでデータに対してはウィルコクソンの符号付き順位検定を行う必要があります．

② 大きいサンプルサイズ
　 サンプル数は大きい方が誤った有意判定を行う可能性が減るため好ましいです．目安としてサンプルサイズが30以上であれば，問題ありません（厳密には，サンプルサイズの決定方法を調べてみてください）．30未満の（サンプルサイズが小さい）場合は ウィルコクソンの符号付き順位検定を行います．