時系列データの特性を調べる方法について，実際の名古屋市の2020年から2022年までの月別平均気温のデータを用いて解説します．
移動平均
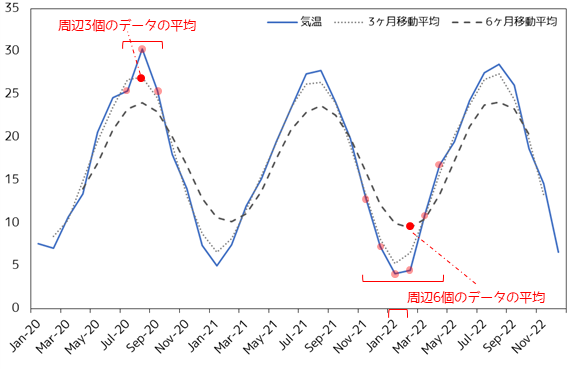
移動平均は，系列データの中の一定の期間（ウィンドウ）における平均値を計算する統計手法です．これにより，データの変動を滑らかにし，長期傾向や季節変動を把握することができます．
例えば，毎月の平均気温データを使った場合を考えてみます．3日間（ウィンドウサイズ＝3）の移動平均を計算すると，毎月の平均気温データを3ヶ月分足し合わせて，その合計を3で割ることになります．これにより，3ヶ月の平均気温が得られます．6ヶ月移動平均のようにウィンドウサイズを大きくするとより滑らかな線が得られ，長期的な傾向を調べることができます．
移動平均にはデータの異常値やノイズを取り除く効果もあります．
移動平均を求める作業を平滑化（スムージング）と言い，平均値をとる移動平均法に加えて，中央値をとる移動中央値法もあります．
中心化移動平均
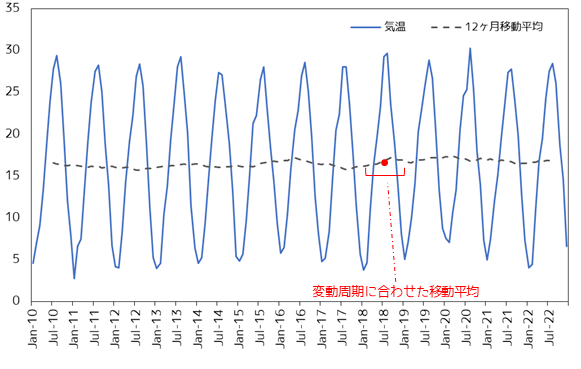
中央化移動平均は移動平均を求める際に，現在のデータ点を中央に位置させます．
例えば12ヶ月移動平均を求めたい場合，ウィンドウサイズが偶数となり移動平均データと時点の対応が適切にとれなくなります．そこで7月時点での移動平均を考える場合，1月から12月までの6.5月時点の移動平均と2月から翌年1月までの7.5月時点の移動平均の2点の平均値をとります．
中央化移動平均は，平滑化を行うためだけでなく季節変動を調整するために使用されます．気温の例では12ヶ月の移動平均をとることで季節変動を取り除いたトレンドを調べることができます．
自己相関係数
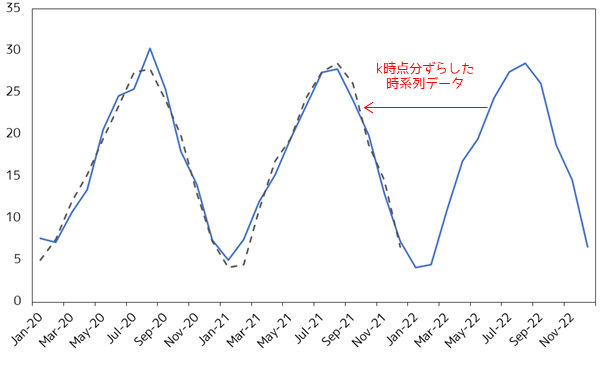
自己相関係数は，ある時点のデータとその一定の時点前のデータとの間の関連性を測る指標です．例えば，過去の一定の時点前のデータと現在のデータが強く関連している場合，自己相関係数は高い値を示します．逆に，過去のデータと現在のデータに関連性がない場合，自己相関係数は低い値を示します．
自己相関係数は，-1から1の範囲を取ります．1に近いほど強い正の自己相関があり，-1に近いほど強い負の自己相関があります．また，0に近い場合は自己相関がほとんどないことを示します．
平均気温の例では，季節変動が明確にあるため12ヶ月分ずらしたデータとの自己相関係数は非常に大きく，グラフの平常もほぼ一致することがわかります．
自己相関係数ある場合は「今月の値には先月の値が影響する」「先月の値には先々月の値が影響する」→「今月の値には先々月の値が関係する」というような推移関係が成立します．したがって，先々月と今月の直接的な影響を調べられていません．
先月の影響を取り除いた関係を調べるためには偏自己相関係数を用います．偏自己相関係数とは，時系列データにおいて過去の時点と現在の時点の相関から，中間の時点の影響を取り除いた相関係数になります．
コレログラム
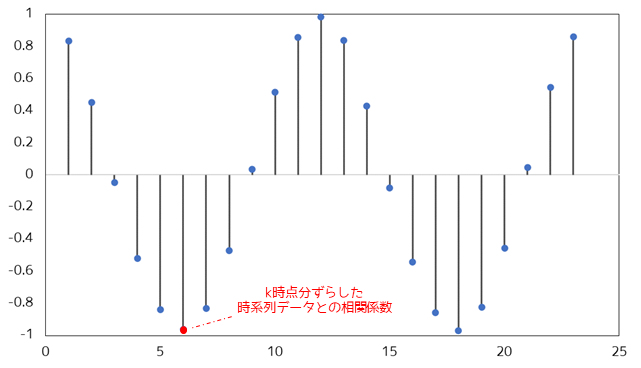
コレログラムでは，横軸にラグkを、縦軸に自己相関係数をとって，ラグごとの自己相関係数の値をグラフ化します．ラグが小さい場合には自己相関係数の値が高く，ラグが大きくなるにつれて徐々に自己相関係数の値が低くなる傾向があります．このようなグラフの形状から，時系列データがどのような性質を持っているのかを把握することができます．
平均気温の例では，ラグが大きくなるにつれて自己相関係数が小さくなり，ラグk=6のときに季節が反対になるため負の相関を示します．ラグk=12のとき再度自己相関係数が大きくなることがわかります．コレログラムから季節変動の周期性を読み取ることができます．
Excelを用いた分析
具体的にExcelを用いた，移動平均・自己相関係数の算出，コレログラムの作成方法を以下のページで紹介しています．
StaatAppを用いた分析
統計解析アプリStaatAppでは，時系列分析の様々な手法を無料で行うことができます．手元のデータを読み込みクリック操作だけで分析できるため，Excelを用いて数式を作成するよりも手軽に行うことができます．
時系列分析について詳しく
時系列分析については考え方や手順など，以下のページで詳しく解説しています．
