中心極限定理について図を用いて解説します.
実践的な中心極限定理の使い方や類似した法則である,大数の法則についても解説しています.
中心極限定理とは
中心極限定理とは統計学・確率論における以下のように定義された法則になります.
『サンプルサイズが大きくなるにつれて,母集団が正規分布でなくても,その平均値の分布は漸近的に正規分布に従う。』
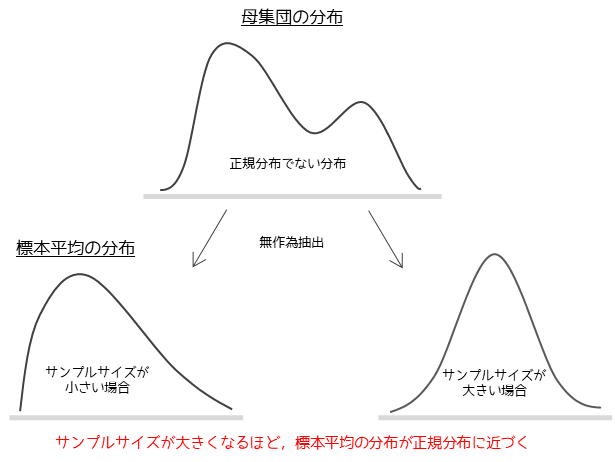
正規分布への近づき方は母集団の分布によって異なります.母集団の分布が正規分布に近い場合は,サンプルサイズが比較的小さくても標本平均の分布は正規分布に近づきます.
母集団の分布が正規分布とかなり異なる場合は,ある程度サンプルサイズが大きくなるまで正規分布に近づきません.どの程度のサンプルサイズで標本平均が正規分布に近似するかは母集団の分布に依存します.
一般的にはn\(\geq\)30の場合に,標本平均の分布は正規分布とみなして統計解析を行うことが多いです.
中心極限定理が成立する標本には,無作為抽出されているという前提条件が必要になります.標本に過度な系統誤差(バイアス)がある場合や,順序データに対しては成立しないことに注意してください.
中心極限定理のよくある間違いとして,「サンプルサイズが大きい場合に母集団もしくは標本の分布が正規分布に近づく」です.
正規分布に近づくのは,複数回標本抽出した場合の標本平均の分布になります.
中心極限定理とは(数学的)
中心極限定理の正確な定義は以下になります.
『Xが平均μ、標準偏差σのある分布に従うならば、サンプルサイズnの無作為標本に基づく標本平均の分布は、nが十分に大きい時、平均μ、分散σ²/nの正規分布に近づく』
特に最後の「平均μ、分散σ²/nの正規分布に近づく」が中心極限定理の活用方法として重要なります.この法則を利用することで,標本平均が母集団の平均μからどれだけずれているかを数学的に評価することができます.
逆に言えばサンプルサイズが大きい場合,標本平均と標準偏差,サンプルサイズだけで母集団の平均値を推定することができます.
t検定と中心極限定理
t検定とは最も代表的な仮説検定で,扱うデータの前提条件として母集団が正規分布に従う必要があります.正規分布に従わない場合にt検定と行うと検出力が下がります(有意差が出にくくなる).
母集団が正規分布に従うかどうかは,身長や体重など既に正規分布従うことが知られているデータ以外では,調べることが難しいもしくは不可能となります.
そこで利用されるのが中心極限定理になります.サンプルサイズが大きい場合は中心極限定理により,母集団が正規分布に従うかが不明の場合にt検定を行っても検出力は下がりにくくなります.
サンプルサイズが大きい場合の基準は一般的には,n\(\geq\)30とすることが多いです.2群で合わせて60以上になります.
中心極限定理を使わず,データに対して直接的に正規性を調べる方法もありますが,個人的にはあまりおすすめはしません.理由としては,サンプルサイズが小さい場合に以下のページで紹介してる手法を用いても微妙な結果しか得られないことと,サンプルサイズが大きい場合でもこれらの手法で確実に正規性があることを証明することはできないからです.
t検定が行えるか判断する際に「正規性があるか」を気にする人が多いです.正規性についてはここまで解説したようにサンプルサイズが大きい場合はあまり気にする必要がありせん.
ただし正しくt検定を行うためには,正規性以外の前提条件に留意する必要があります.t検定は平均値を扱う検定であるため,数量データに対して行うことが可能で順位データに対しては実施することができません.また,中心極限定理の前提条件でもある無作為抽出された標本である必要もあります.
大数の法則
中心極限定理と類似した法則として大数の法則があります.大数の法則は以下のように定義されます.
『試行回数が大きくなるほど,経験的確率が理論的確率に従う』
例えばコインを投げて表裏になる確率は,投げる回数が多いほど0.5に近づくという意味になります.この法則は日常的にも感じる現象で,不完全情報ゲームを何回も繰り返すと本当の実力が反映された結果に収束にするみたいなことです.
大数の法則は数学的に証明されている法則になります.
大数の法則を標本平均に当てはめると,サンプルサイズが大きくなるほど標本平均は母平均に近づくことを意味します.









