分布に差があるかを調べるために行う,コルモゴロフ・スミルノフ検定について紹介します.
1標本の場合と2標本の場合の違いや,Excelを用いた計算方法も紹介しています.
コルモゴロフ・スミルノフ検定とは
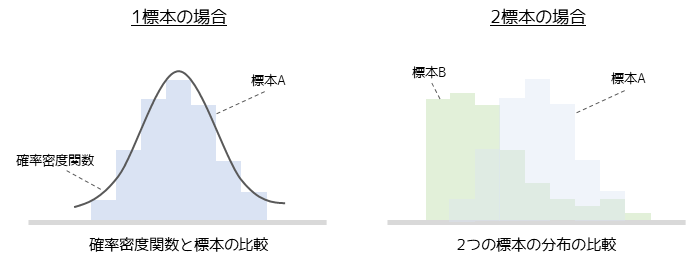
コルモゴロフ・スミルノフ検定(K-S検定)は2つの母集団の確率分布が異なるかを調べる手法になります.1標本に対して行う場合と,2標本に対して行う2つのパターンがあります.
1標本の場合は一般的な確率分布(正規分布やポアソン分布)と標本の分布の差を調べることができます.よくある活用方法として,正規分布と標本を比較することで標本の正規性を調べる場合に用いられます.
2標本の場合は2標本の差を調べるために用いられます.母集団が確率分布に従うという仮定が不要なノンパラメトリック検定の1つになります.
1標本のコルモゴロフ・スミルノフ検定
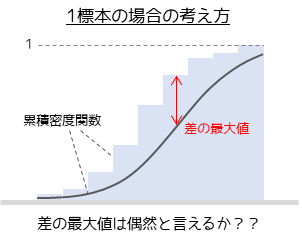
1標本の場合は標本と一般的な確率分布との比較を行います.標本と確率分布の累積密度関数の差の最大値を検定統計量の計算に用います.
累積密度関数の差の最大値が大きいほど検定統計量も大きくなり,比較した標本の分布と一般的な確率分布は異なると判断することができます.
例えば,正規分布と比較する場合の帰無仮説は「標本の確率分布と正規分布は等しい」となり,対立仮説は「標本の確率分布と正規分布は異なる」となります.コルゴモロフ・スミルノフ検定の結果有意差がある場合は,対立仮説の「標本の確率分布と正規分布は異なる」といった結論が得られます.
2標本のコルモゴロフ・スミルノフ検定
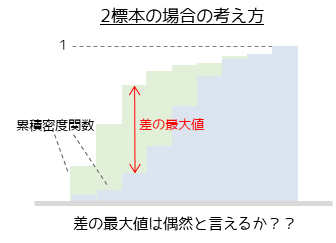
2標本の場合は任意の2つ標本の分布の比較を行います.2つの標本の累積密度関数を比較して差の最大値を検定統計量の計算に用います.
累積密度関数の差の最大値が大きいほど検定統計量も大きくなり,比較した2標本の分布は異なると判断することができます.コルゴモロフ・スミルノフ検定では2標本のサンプルサイズが異なる場合でも検定可能です.
帰無仮説は「2つの標本の分布は等しい」,対立仮説は「2つの標本の分布は異なる」と設定します.
Excelで行う2標本のコルモゴロフ・スミルノフ検定
2標本のコルゴモロフ・スミルノフ検定について,Excelで行う方法を紹介しまします.
例として,1から100までの間の値をランダムに発生させて標本Aと標本Bを比較します.下記のような表を作成して検定統計量Kを算出します.(説明のため見切れていますが,各標本のサンプルサイズは100になります.)
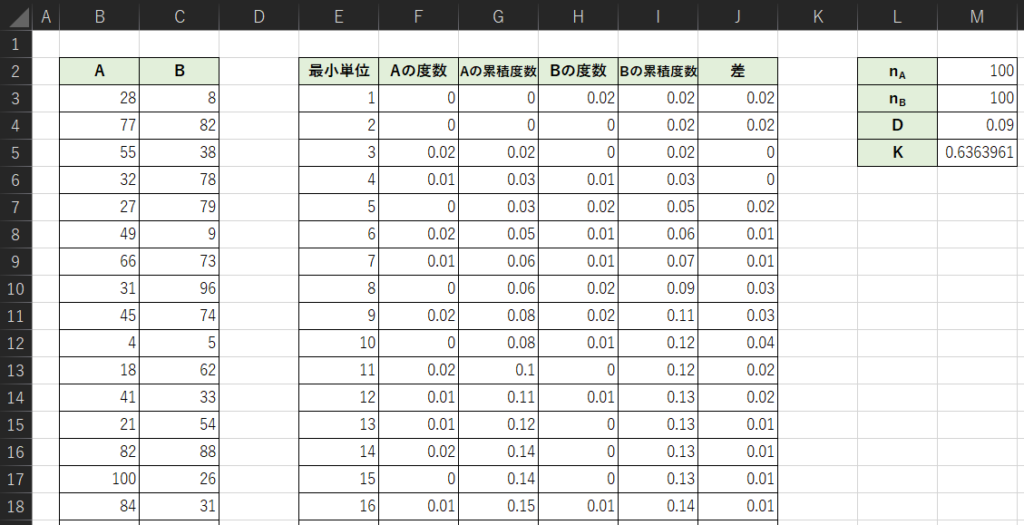
各セルの入力式は以下のようになります.
・F列:=COUNTIF(B$3:B$102,E3)/$M$2 ※ 3行目のセルの数式です.下の行へは数式のコピーを行ってください.
・G3:=F3
・G列:=G3+F4 ※ 4行目のセルの数式です.
・H列:=COUNTIF(C$3:C$102,E3)/$M$3
・I3:=H3
・I列:=I3+H4 ※ 4行目のセルの数式です.
・J列:=ABS(G3-I3)
・M4:=MAX(J3:J102)
・M5:=M4*SQRT((M2*M3)/(M2+M3))
各セルの入力式について解説します.
① データの入力【B列】【C列】
比較する標本のデータを2つの列に入力します.
② 最小値から最大値までの連続値の入力【E列】
2つ標本の度数を計算するために,最小値から最大値までの連続値を入力します.
例では最小値が”1”で最大値が”100”なので,1から100までの値を”1”刻みで入力します.小数点以下の値が含まれる場合は,その桁数に従って連続値を入力します.3行目以降を入力する際はExcelのオートフィル機能を使ってください.
③ 標本Aの度数を求める【F列】
②で入力した値ごとに標本Aの度数を算出します.Excelでは条件に一致する値の数(度数)を計算するために,COUNTIF関数を使用します.
F3セルに入力した式を②で入力した行数分オートフィル機能でコピーします.
④ 標本Aの累積度数を求める【G3】【G列】
標本Aの累積度数を算出します.累積度数は③で求めた度数を1行ずつ足すことで算出します.
G列の最終行の値が”1”になれば,F列G列の計算結果は正しいと判断できます.
⑤ 標本Bの度数・累積度数を求める【H列】【I3】【I列】
③④と同じ手順で標本Bの度数・累積度数を算出します.
⑥ 累積度数の差の絶対値を求める【J列】
標本Aと標本Bの累積度数の差の絶対値を算出します.ExcelではABS関数を用いて絶対値を計算できます.
⑦ 差の最大値を求める【M4】
検定統計量を計算するために必要な累積度数の差の最大値Dを算出します.Excelでは最大値をMAX関数を用いて計算することができます.
⑧ 検定統計量を求める【M5】
コルゴモロフ・スミルノフ検定の検定統計量Kを算出します.検定統計量は以下の式で求めることができます.
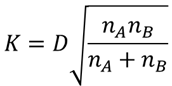
⑨ 検定統計量と限界値を比較する
算出した検定統計量と限界値を比較して有意差判定を行います.コルゴモロフ・スミルノフ検定の検定表は以下のようになります.
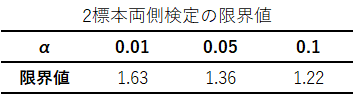
有意水準α=0.05とすると限界値は1.36になります.検定統計量Kは0.636…であったので限界値\(\geq\)検定統計量となり,帰無仮説は棄却されません.
以上が,2標本の場合のExcelを用いたコルゴモロフ・スミルノフ検定になります.
補足① コルモゴロフ・スミルノフ検定のよくある間違い
1標本のコルゴモロフ・スミルノフ検定は,標本の正規性を調べるためによく用いられます.検定結果として有意差がない場合に「標本の母集団の分布は正規分布に従う」と解釈されがちです.
この解釈は仮説検定の基本的な使い方として誤りになります.仮説検定では有意差がない(帰無仮説が棄却されない)場合,帰無仮説が積極的に採択される訳ではありません.
標本の分布と正規分布を比較して有意差がない場合は「標本の分布は正規分布と異なるとは言えない」といった結論になります.









