カイ二乗検定でよく使われる,独立性の検定と適合度の検定について具体的な計算例を用いて説明します.
実際に行う際は,用いるデータの前提条件についても確認してみてください.
独立性の検定
独立性の検定では,2つの変数に関連性があるかを判断する際に用います.特に,クロス集計表を作成した後に項目ごと(表側と表頭)に関連性があるか調べる際によく用います.
では,具体的のどのような手順で計算していくかを例を用いて説明します.
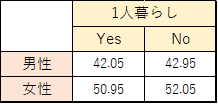
大学生を対象に「1人暮らしをしているかどうか」というアンケートを取り,アンケート結果から以下のような2×2クロス集計表を作成したとします.
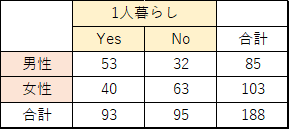
ここで,性別は1人暮らしをしていることに関連性があるか(性別によって差があるか)調べたい場合に独立性の検定を行います.
検定を行う際にまず,各セルの期待度数を求めます.期待度数とは,変数間で独立性がある場合このような値になるであろうといった値です.
期待度数の求め方を説明するために,クロス集計表のセルに以下のような記号を振ります.
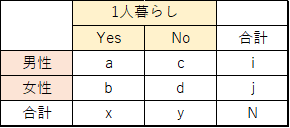
そして,各セルの期待度数は以下の式で求めることができます.A~Dはそれぞれのセルの期待度数です.
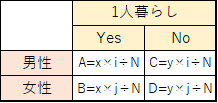
各セルの期待度数を求めたら,次はカイ二乗統計量を求めます.カイ二乗統計量は以下の式で求めることができます.
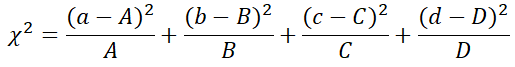
カイ二乗統計量は,対応した各セルの観測度数ー期待度数の2乗を期待度数で割った値の総和になります.今回の例ではカイ二乗統計量は”10.3”となりました.
最後に,求めたカイ二乗統計量とカイ二乗分布表を用いてp値を求めます.
2×2クロス集計表の場合自由度は1となるので,カイ二乗分布表の一番上の列を見ます.そして,カイ二乗統計量が”6.64″より大きいことからp値は0.01より小さいことが分かります.

独立性の検定ではp値が0.05以下の場合(有意水準が0.05),関連性があると言えます.今回の場合は「1人暮らしかどうかと性別の間に関連性があると言える」ということが分かりました.
ここまでの独立性の検定の手順をまとめると以下になります.
① 各セルの期待度数を計算する
② 観測度数と期待度数を用いてカイ二乗統計量を計算する
③ カイ二乗分布とカイ二乗統計量を用いてp値を探す
④ p値が0.05以下の場合,変数は独立していると言える
実際の計算ではExcelを用いると,手順の①②で作成した表と”CHISQ.TEST関数”を用いることでカイ二乗統計量を計算せずに,p値を求めることが可能です.
適合度の検定
適合度の検定とは,期待度数に対して実際の観測度数のあてはまりの良さを検定する手法です.
検定の手順を簡単に説明すると,独立性の検定で説明した期待度数が既に分かっている場合の検定です.
ここからは具体例を用いて適合度の検定の手順を説明します.
企業Xにおいてある年に採用された社員の出身大学の割合を集計したとします.その企業の社員全体の出身大学の割合についても同様に集計して求めることができます.このとき,観測度数がある年に採用された社員の出身大学,期待度数が社員全体の出身大学とみなします.
集計結果は以下のようになりました.

期待度数が既知であり,観測度数は期待度数に対してどれぐらい当てはまっているのかを検定します.
期待度数が既知であるので,カイ二乗統計量を求めます.カイ二乗統計の求め方は, 対応した観測度数ー期待度数の2乗を期待度数で割った値の総和になります.
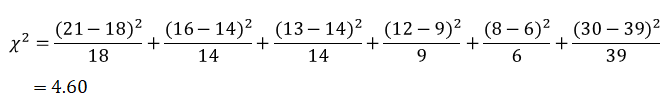
カイ二乗統計量が”4.60”と求められたので,あとはカイ二乗分布を用いてp値を探します.今回の例では,項目数が6になるので自由度5のカイ二乗分布を見ます.

カイ二乗分布表から”4.60″は,p値が0.9から0.1の間であることが分かります.このことから,有意水準を0.05とした場合,観測度数は期待度数に当てはまっていると言えます.
今回の例では,「企業Xのある年に採用された社員の出身大学の割合は,社員全体の割合と有意差はないと言える」ということになります.
適合度の検定の手順をまとめると以下になります.
① 観測度数と期待度数を用いてカイ二乗統計量を計算する
② カイ二乗分布とカイ二乗統計量を用いてp値を探す
③ p値が0.05以下の場合,観測データは理論値に当てはまっていると言える
カイ二乗検定の前提条件
ここまでは,カイ二乗検定を実際にどのような手順で計算するのかを説明しました.最後に,カイ二乗検定を行う際に用いるデータの前提条件について説明します.
① カテゴリカルデータ
カイ二乗検定で用いるデータはカテゴリカルデータである必要があります.カイ二乗検定を行う前に作成するクロス集計表自体もカテゴリカルデータであることが作成する前提条件となります.
② 累積度数
アンケートを行い,割合を用いて集計した結果には用いることができません.クロス集計表でも同様に,ある項目に対して何人いたかといった度数で表現したデータが前提条件です.
③ 期待度数の最小値が5以上
クロス集計表を作成した際に,各セルの値が5以上であることがカイ二乗検定を行う前提条件です.5未満のセル(正確には期待度数)がある場合は,フィッシャーの正確性検定を使用します.
おわりに
カイ二乗検定の手順について計算例を用いて説明しました.Excelを用いてカイ二乗検定を行う手順は下記ページで解説しているので参考にしてください.
2×2クロス集計表の検定を行う際は,Excelを用いて検定を行うのが一番便利です.しかし,項目数が多い場合はExcelでは期待度数を求めるのが大変ですので,RもしくはPythonを用いて計算しましょう!